
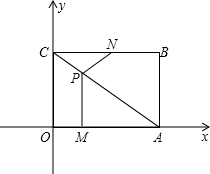
 如图,平面直角坐标系中,四边形OABC为矩形,点A,B的坐标分别为(4,0),(4,3),动点M,N分别从O,B同时出发.以每秒1个单位的速度运动.其中,点M沿OA向终点A运动,点N沿BC向终点C运动.其中,点M沿OA向终点A运动,点N沿BN向终点C运动.过点M作MP⊥OA,交AC于P,连接NP,设M、N运动的时间为t秒(0<t<4).
如图,平面直角坐标系中,四边形OABC为矩形,点A,B的坐标分别为(4,0),(4,3),动点M,N分别从O,B同时出发.以每秒1个单位的速度运动.其中,点M沿OA向终点A运动,点N沿BC向终点C运动.其中,点M沿OA向终点A运动,点N沿BN向终点C运动.过点M作MP⊥OA,交AC于P,连接NP,设M、N运动的时间为t秒(0<t<4).分析 (1)先确定出点C坐标,进而得出直线AC解析式,即可得出点P的坐标,最后用两点间的距离公式即可得出结论;
(2)先得出AC=5,BN=t,CN=4-t,用相似三角形的性质列出方程即可求出时间t;
(3)由菱形的性质,邻边相等即可分三种情况列方程即可求出时间t.
解答 解:(1)∵四边形OABC为矩形,点A,B的坐标分别为(4,0),(4,3),
∴C(0,3),∴直线AC解析式为y=-$\frac{3}{4}$x+3,
∵点M从点O向点A以每秒1个单位的速度运动,
∴OM=t,当x=t时,y=-$\frac{3}{4}$t+3,
∴P(t,-$\frac{3}{4}$t+3),
∵C(0,3),
∴CP=$\sqrt{{t}^{2}+(-\frac{3}{4}t+3-3)^{2}}$=$\frac{5}{4}$t,
故答案为:t,-$\frac{3}{4}$t+3,$\frac{5}{4}$t,
(2)∵A(4,0),B(4,3),
∴OA=BC=4,OB=3,
∴AC=5,
由运动知,BN=t,
∴CN=4-t,
由(1)知,CP=$\frac{5}{4}$t,
∵∠ACB=∠PCN,以C、P、N为顶点的三角形与△ABC相似,
∴①当$\frac{BC}{CN}=\frac{AC}{CP}$时,
∴$\frac{4}{4-t}=\frac{5}{\frac{5}{4}t}$,
∴t=2,
②当$\frac{BC}{CP}=\frac{AC}{CN}$时,
∴$\frac{4}{\frac{5}{4}t}=\frac{5}{4-t}$,
∴t=$\frac{64}{41}$,
∴t为2或$\frac{64}{41}$时,以C、P、N为顶点的三角形与△ABC相似.
(3)由(1)知,CP=$\frac{5}{4}$t,P(t,-$\frac{3}{4}$t+3),
由(2)知,CN=4-t,
∴N(4-t,3),
∴PN=$\sqrt{(4-t-t)^{2}+(3+\frac{3}{4}t-3)^{2}}$=$\sqrt{(2t-4)^{2}+{\frac{9}{16}t}^{2}}$,
∵以C、P、N、E为顶点的四边形是菱形,
∴①当CP=CN时,
∴$\frac{5}{4}$t=4-t,
∴t=$\frac{16}{9}$,
②当 CP=PN时,$\frac{5}{4}$t=$\sqrt{(2t-4)^{2}+{\frac{9}{16}t}^{2}}$,
∴t=4(舍)或t=$\frac{4}{3}$
③当CN=PN时,4-t=$\sqrt{(2t-4)^{2}+{\frac{9}{16}t}^{2}}$,
∴t=0(舍)或t=$\frac{128}{57}$,
以C、P、N、E为顶点的四边形是菱形时,t的值为$\frac{16}{9}$或$\frac{4}{3}$或$\frac{128}{57}$秒.
点评 此题是相似三角形综合题,主要考查了平面坐标系内两点间的公式,相似三角形的性质,菱形的性质,解本题的关键分类讨论思想,是一道比较简单的中考常考题.


科目:初中数学 来源: 题型:解答题
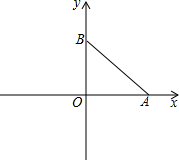 如图,在平面直角坐标系中,O为坐标原点,A、B两点的坐标分别为
如图,在平面直角坐标系中,O为坐标原点,A、B两点的坐标分别为查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
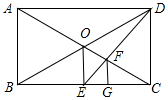 如图,在矩形ABCD中,对角线AC,BD相交于点O,OE⊥BC于点E,连接DE交OC于点F,作FG⊥BC于点G,则线段BG与GC的数量关系是BG=2CG.
如图,在矩形ABCD中,对角线AC,BD相交于点O,OE⊥BC于点E,连接DE交OC于点F,作FG⊥BC于点G,则线段BG与GC的数量关系是BG=2CG.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com