
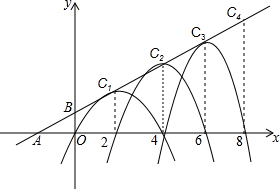
 如图,在平面直角坐标系中,A(-2,0),B(0,1),有一组抛物线ln,它们的顶点Cn(xn.yn)在直线AB上,并且经过(xn+1,0),当n=1,2,3,4…时,xn=2,4,6,8…根据上述规律,写出抛物线l7的表达式为y=-$\frac{23}{2}$(x-2)2+$\frac{23}{2}$或y=-$\frac{23}{2}$x2+46x-$\frac{69}{2}$.
如图,在平面直角坐标系中,A(-2,0),B(0,1),有一组抛物线ln,它们的顶点Cn(xn.yn)在直线AB上,并且经过(xn+1,0),当n=1,2,3,4…时,xn=2,4,6,8…根据上述规律,写出抛物线l7的表达式为y=-$\frac{23}{2}$(x-2)2+$\frac{23}{2}$或y=-$\frac{23}{2}$x2+46x-$\frac{69}{2}$. 分析 根据A(-2,0),B(0,1)的坐标求直线AB的解析式为y=$\frac{1}{2}$x+1,因为顶点C1的在直线AB上,C1坐标可求;根据横坐标的变化规律可知,C7的横坐标为21,代入直线AB的解析式y=$\frac{1}{2}$x+1中,可求纵坐标.
解答 解:设直线AB的解析式为y=kx+b(k≠0).
则$\left\{\begin{array}{l}{-2k+b=0}\\{b=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=1}\end{array}\right.$,
∴直线AB的解析式为y=$\frac{1}{2}$x+1
∵抛物线L1的顶点C1的横坐标为2,且顶点在直线AB上,
∴y1=$\frac{1}{2}$×2+1=2.
则C1(2,2).
∵对称轴与x轴的交点的横坐标依次为2,4,6,8…
∴每个数都比前个数多2,
∴抛物线L7的顶点C7的横坐标为14,
则y7=$\frac{1}{2}$×14+1=8.
∴抛物线L7的顶点坐标为:(14,8).
同理,由抛物线L7经过点(12,0),求得该抛物线的解析式为:y=-$\frac{23}{2}$(x-2)2+$\frac{23}{2}$或y=-$\frac{23}{2}$x2+46x-$\frac{69}{2}$.
故答案是:y=-$\frac{23}{2}$(x-2)2+$\frac{23}{2}$或y=-$\frac{23}{2}$x2+46x-$\frac{69}{2}$.
点评 此题考查了待定系数法求一次函数的解析式,还考查了点与函数关系式的关系,考查了学生的分析归纳能力.


科目:初中数学 来源: 题型:解答题
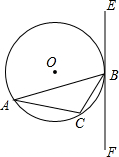 已知:△ABC内接于⊙O,过点B作直线EF,AB为非直径的弦,且EF是⊙O的切线
已知:△ABC内接于⊙O,过点B作直线EF,AB为非直径的弦,且EF是⊙O的切线查看答案和解析>>
科目:初中数学 来源: 题型:填空题
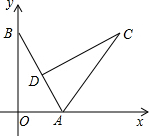 如图,平面直角坐标系中,已知O为坐标原点,A(3,0),B(0,4).将Rt△AOB绕点A顺时针旋转得到Rt△ACD,旋转后点D恰好落在AB边上时,则D点的坐标为($\frac{6}{5}$,$\frac{12}{5}$).
如图,平面直角坐标系中,已知O为坐标原点,A(3,0),B(0,4).将Rt△AOB绕点A顺时针旋转得到Rt△ACD,旋转后点D恰好落在AB边上时,则D点的坐标为($\frac{6}{5}$,$\frac{12}{5}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 定义{A,B,C}为函数y=ax2+bx+c的“特征数”.如:函数y=x2-2x-3的“特征数”是{1,-2,-3},函数y=2x+4的“特征数”是{0,2,4},函数y=-x的“特征数”是{0,-1,0}.
定义{A,B,C}为函数y=ax2+bx+c的“特征数”.如:函数y=x2-2x-3的“特征数”是{1,-2,-3},函数y=2x+4的“特征数”是{0,2,4},函数y=-x的“特征数”是{0,-1,0}.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1.
如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,点M的坐标是(5,4),⊙M与y轴相切于点C,与x轴相交于A,B两点.
如图,在平面直角坐标系中,点M的坐标是(5,4),⊙M与y轴相切于点C,与x轴相交于A,B两点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 图象必经过点(1,2) | B. | y随x的增大而减少 | ||
| C. | 图象在第一、三象限 | D. | 若x>1,则y<2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 江阴市明天将有20%的地区降水 | B. | 江阴市明天将有20%的时间降水 | ||
| C. | 江阴市明天降水的可能性较小 | D. | 江阴市明天肯定不降水 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$$\sqrt{2}$)2=1 | B. | $\sqrt{(-6)^{2}}$=6 | C. | $\sqrt{{5}^{2}}$=±5 | D. | (3$\sqrt{2}$)2=6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com