
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2 , 请直接写出旋转中心的坐标;
(3)在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
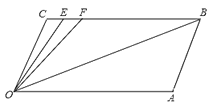
【题目】如图,CB∥OA,∠C=∠OAB=124°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF,∠OEC=∠COB,则∠OEC=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 的直径
的直径![]() ,
,![]() ,
,![]() 是
是![]() 的两条切线,
的两条切线,![]() 切
切![]() 于
于![]() ,交
,交![]() 于
于![]() ,设
,设![]() ,
,![]() ,
,![]() .
.
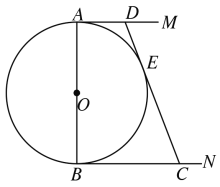
(1)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)若![]() ,
,![]() 是
是![]() 的两实根,求
的两实根,求![]() ,
,![]() 的值;
的值;
(3)在(2)的前提下,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】谁更合理?
某种牙膏上部圆的直径为2.6cm,下部底边的长为4cm,如图,现要制作长方体的牙膏盒,牙膏盒底面是正方形,在手工课上,小明、小亮、小丽、小芳制作的牙膏盒的高度都一样,且高度符合要求.不同的是底面正方形的边长,他们制作的边长如下表:
制作者 | 小明 | 小亮 | 小丽 | 小芳 |
正方形的边长 | 2cm | 2.6cm | 3cm | 3.4cm |
(1)这4位同学制作的盒子都能装下这种牙膏吗?(![]() )
)
(2)若你是牙膏厂的厂长,从节约材料又方便取放牙膏的角度来看,你认为谁的制作更合理?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图OA平分∠BAC,∠1=∠2.
求证:AO⊥BC.
同学甲说:要作辅助线;
同学乙说:要应用角平分线性质定理来解决:
同学丙说:要应用等腰三角形“三线合一”的性质定理来解决.
请你结合同学们的讨论写出证明过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2﹣2x+3的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.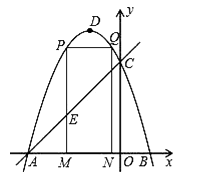
(1)求点A、B、C的坐标;
(2)点M(m,0)为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N,可得矩形PQNM.如图,点P在点Q左边,试用含m的式子表示矩形PQNM的周长;
(3)当矩形PQNM的周长最大时,m的值是多少?并求出此时的△AEM的面积;
(4)在(3)的条件下,当矩形PMNQ的周长最大时,连接DQ,过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方).若FG= ![]() DQ,求点F的坐标.
DQ,求点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
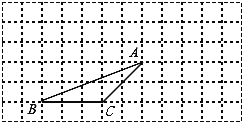
【题目】如图,△ABC的顶点都在方格纸的格点上,将△ABC向右平移4格,再向上平移2格,其中每个格子的边长为1个单位长度。
⑴在图中画出平移后的△A′B′C′;
⑵若连接AA′、CC′,则这两条线段的关系是 ;
⑶作△ABC的高AD,并求△ABC的面积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com