
【题目】如图,在□ABCD中,点E、F分别是AD、BC的中点,分别连接BE、DF、BD.
(1)求证:△AEB≌△CFD;
(2)若四边形EBFD是菱形,求∠ABD的度数.

【答案】(1)、证明过程见解析;(2)、90°
【解析】试题分析:(1)、根据平行四边形的性质和已知条件证明即可;(2)、由菱形的性质可得:BE=DE,因为∠EBD+∠EDB+∠A+∠ABE=180°,所以∠ABD=∠ABE+∠EBD=![]() ×180°=90°,问题得解.
×180°=90°,问题得解.
试题解析:(1)、∵四边形ABCD是平行四边形, ∴∠A=∠C,AD=BC,AB=CD.
∵点E、F分别是AD、BC的中点, ∴AE=![]() AD,FC=
AD,FC=![]() BC. ∴AE=CF.
BC. ∴AE=CF.
∴△AEB≌△CFD(SAS).
(2)、∵四边形EBFD是菱形, ∴BE=DE. ∴∠EBD=∠EDB. ∵AE=DE, ∴BE=AE.
∴∠A=∠ABE. ∵∠EBD+∠EDB+∠A+∠ABE=180°, ∴∠ABD=∠ABE+∠EBD=![]() ×180°=90°.
×180°=90°.


科目:初中数学 来源: 题型:
【题目】小天想要计算一组数据92,90,94,86,99,85的方差S02,在计算平均数的过程中,将这组数据中的每一个数都减去90,得到一组新数据2,0,4,﹣4,9,﹣5,记这组新数据的方差为S12,则S12__S02(填“>”,“=”或”<”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有公路l1同侧、l2异侧的两个城镇A,B,电信部门要在S区修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条公路l1,l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置.(保留作图痕迹,不写作法)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点P(-3,4) 关于y 轴的对称点的坐标为(
A. (4,-3) B. (3,-4) C. (3,4) D. ( 3,-4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a,b为有理数,若a99b100<0,且a﹣b>0.则下列推断正确的是( )
A. a>0,b>0 B. a>0,b<0 C. a<0,b>0 D. a<0,b<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两地相距500千米,汽车从甲地以每小时80千米的速度开往乙地.
(1)写出汽车离乙地的距离s(千米)与开出时间t(小时)之间的函数关系式,并指出是不是一次函数;
(2)写出自变量的取值范围;
(3)汽车从甲地开出多久,离乙地为100千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
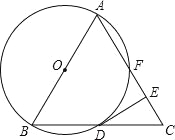
【题目】如图,已知△ABC是等边三角形,以AB为直径作⊙O,交BC边于点D,交AC边于点F,作DE⊥AC于点E.
(1)求证:DE是⊙O的切线;
(2)若△ABC的边长为4,求EF的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com