
分析 (1)设购买一个足球需要x元,购买一个篮球需要y元,根据购买2个足球和3个篮球共需340元,购买5个足球和2个篮球共需410元,列方程组求解,然后设折扣为m,根据打折之后购买6个足球和3个篮球仅需432元列方程求解;
(2)设购买a个篮球,则购买(50-a)个足球,根据总费用不超过2250,列不等式求出最大整数解.
解答 解:(1)设购买一个足球需要x元,购买一个篮球需要y元,
根据题意得:$\left\{\begin{array}{l}{2x+3y=340}\\{5x+2y=410}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=50}\\{y=80}\end{array}\right.$,
设折扣为m,
则有,(6×50+3×80)m=432,
解得:m=0.8,
答:店庆期间超市的折扣是八折;
(2)设购买a个篮球,则购买(50-a)个足球,
根据题意得:[80a+50(50-a)]×0.8≤2250,
解得:a≤$\frac{125}{12}$,
∵a是整数,
∴a≤10,
答:最多可以购买10个篮球.
点评 本题考查了二元一次方程组的应用和一元一次不等式的应用,解答本题的关键是读懂题意,找出合适的等量关系和不等关系,列方程和不等式求解.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:初中数学 来源: 题型:选择题
| A. | ① | B. | ② | C. | ③ | D. | ④ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
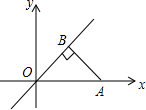 如图,点A的坐标是(2,0),AB垂直于直线y=x于点B,则B点的坐标是( )
如图,点A的坐标是(2,0),AB垂直于直线y=x于点B,则B点的坐标是( )| A. | (1,$\sqrt{2}$) | B. | (1,1) | C. | ($\sqrt{2}$,$\sqrt{2}$) | D. | (1,$\sqrt{2}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对角线互相平分的四边形是平行四边形 | |
| B. | 对角线相等的四边形是矩形 | |
| C. | 对角线互相垂直平分的四边形是菱形 | |
| D. | 对角线互相垂直平分且相等的四边形是正方形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com