
【题目】一块试验田的形状如图,已知:∠ABC=90°,AB=4m,BC=3m,AD=12m,CD=13m.求这块试验田的面积.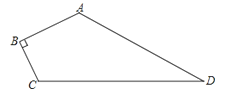
【答案】解:连接AC,如图所示:
∵∠B=90°,∴△ABC为直角三角形,
又AB=4,BC=3,
∴根据勾股定理得:AC=5,
又AD=12,CD=13,
∴AD2=122=144,CD2+AC2=122+52=144+25=169,
∴CD2+AC2=AD2 ,
∴△ACD为直角三角形,∠ACD=90°,
则S四边形ABCD=S△ABC+S△ACD=![]() ABBC+
ABBC+![]() ACCD=36.
ACCD=36.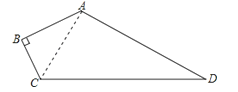
【解析】连接AC,在直角三角形ABC中,由AB及BC的长,利用勾股定理求出AC的长,再由AD及CD的长,利用勾股定理的逆定理得到三角形ACD为直角三角形,根据四边形ABCD的面积=直角三角形ABC的面积+直角三角形ACD的面积,即可求出四边形的面积.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对勾股定理的逆定理的理解,了解如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形.


科目:初中数学 来源: 题型:
【题目】科学家在实验中检测出某微生物约为0.0000025米,将0.0000025用科学记数法表示为( )
A.2.5×10﹣6
B.2.5×106
C.2.5×10﹣5
D.25×10﹣5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,ABCD中,BE,CF分别是∠ABC和∠BCD的一平分线,BE,CF相交于点O.
(1)求证:BE⊥CF;
(2)试判断AF与DE有何数量关系,并说明理由;
(3)当△BOC为等腰直角三角形时,四边形ABCD是何特殊四边形?
(直接写出答案)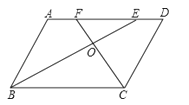
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】台风是一种自然灾害,它以台风中心为圆心,在周围数十千米范围内形成气旋风暴,有极强的破坏力.今年首个超强台风“圣帕”第0709号超强台风于8月13日在北纬21.3度,东经123.3度的太平洋上生成,其中心气压925百帕,近中心最大风速55米/秒,生成时还是热带风暴的“圣帕”,在连跳两级后,15日晚8时已“变身”为超强台风.向台湾东部沿海逼近并登陆台湾岛,之后于19日上午将在福建中南部沿海福州一带再次登陆.在这之前,台风中心在我国台湾海峡的B处,在沿海城市福州A的正南方向240千米,其中心风力为12级,每远离台风中心25千米,台风就会减弱一级,如图所示,该台风中心正以20千米/时的速度沿北偏东30°方向向C移动,且台风中心的风力不变,若城市所受风力达到或超过4级,则称受台风影响.试问:
(1)该城市是否会受到台风影响?请说明理由.
(2)若会受到台风影响,那么台风影响该城市的持续时间有多长?
(3)该城市受到台风影响的最大风力为几级?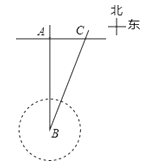
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图象经过点A(﹣1,4),B(1,0),
的图象经过点A(﹣1,4),B(1,0),![]() 经过点B,且与二次函数
经过点B,且与二次函数![]() 交于点D.
交于点D.
(1)求二次函数的表达式;
(2)点N是二次函数图象上一点(点N在BD上方),过N作NP⊥x轴,垂足为点P,交BD于点M,求MN的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com