
【题目】已知:在![]() 中,
中,![]() .
.
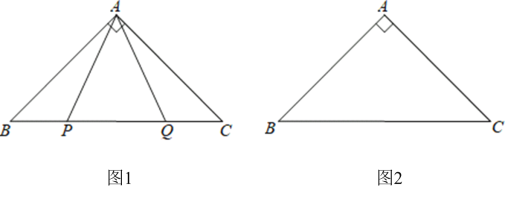
(1)如图1,![]() 是
是![]() 边上两点,
边上两点,![]() , 求
, 求![]() 的度数.
的度数.
(2)点![]() 是
是![]() 边上两动点(不与
边上两动点(不与![]() 重合), 点
重合), 点![]() 在点
在点![]() 左侧,且
左侧,且![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,连接
,连接![]() .
.
①依题意将图2补全.
②小明通过观察和实验,提出猜想:在点![]() 运动的过程中,始终有
运动的过程中,始终有![]() 为等腰直角三角形,他把这个猜想与同学们进行交流,通过讨论,形成以下证明猜想的思路:要想证明
为等腰直角三角形,他把这个猜想与同学们进行交流,通过讨论,形成以下证明猜想的思路:要想证明![]() 为等腰直角三角形,只需证
为等腰直角三角形,只需证![]() .
.
请参考上面的思路,帮助小明证明△APM 为等腰直角三角形.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(问题背景)如图1所示,在![]() 中,
中,![]() ,
,![]() ,点D为直线
,点D为直线![]() 上的个动点(不与B、C重合),连结
上的个动点(不与B、C重合),连结![]() ,将线段
,将线段![]() 绕点D按顺时针方向旋转90°,使点A旋转到点E,连结
绕点D按顺时针方向旋转90°,使点A旋转到点E,连结![]() .
.
(问题初探)如果点D在线段![]() 上运动,通过观察、交流,小明形成了以下的解题思路:过点E作
上运动,通过观察、交流,小明形成了以下的解题思路:过点E作![]() 交直线
交直线![]() 于F,如图2所示,通过证明
于F,如图2所示,通过证明![]() ______,可推证
______,可推证![]() 是_____三角形,从而求得
是_____三角形,从而求得![]() ______°.
______°.
(继续探究)如果点D在线段![]() 的延长线上运动,如图3所示,求出
的延长线上运动,如图3所示,求出![]() 的度数.
的度数.
(拓展延伸)连接![]() ,当点D在直线
,当点D在直线![]() 上运动时,若
上运动时,若![]() ,请直接写出
,请直接写出![]() 的最小值.
的最小值.
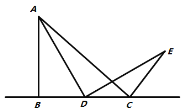
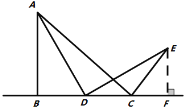
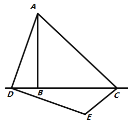
图1 图2 图3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车在某次行驶过程中,油箱中的剩余油量y(升)与行驶路程x(千米)之间是一次函数关系,其部分图象如图所示.
(1)求y关于x的函数关系式;(不需要写定义域)
(2)已知当油箱中的剩余油量为8升时,该汽车会开始提示加油,在此次行驶过程中,行驶了500千米时,司机发现离前方最近的加油站有30千米的路程,在开往该加油站的途中,汽车开始提示加油,这时离加油站的路程是多少千米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场某种商品平均每天可销售30件,每件盈利50元。为了尽快减少库存,商场决定采取适当的降价措施。经调查发现,每件商品每降价1元,商场平均每天可多售出2件。设每件商品降价![]() 元。据此规律,请回答:
元。据此规律,请回答:
(1)商场日销售量增加_____件,每件商品盈利_____元(用含![]() 的代数式表示)。
的代数式表示)。
(2)在上述条件不变、销售正常情况下,每件商品降价多少元时,商场日盈利可达到2100元?
查看答案和解析>>
科目:初中数学 来源: 题型:
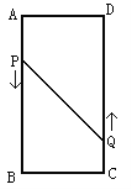
【题目】如图,矩形![]() 的中,
的中,![]() ,
,![]() ,动点
,动点![]() 、
、![]() 分别以
分别以![]() 、
、![]() 的速度从点
的速度从点![]() 、
、![]() 同时出发,点
同时出发,点![]() 从点
从点![]() 向点
向点![]() 移动.
移动.
(1)若点![]() 从点
从点![]() 移动到点
移动到点![]() 停止,点
停止,点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 同时出发,问经过
同时出发,问经过![]() 时
时![]() 、
、![]() 两点之间的距离是多少
两点之间的距离是多少![]() ?
?
(2)若点![]() 从点
从点![]() 移动到点
移动到点![]() 停止,点
停止,点![]() 随之停止移动,点
随之停止移动,点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 同时出发,问经过多长时间
同时出发,问经过多长时间![]() 、
、![]() 两点之间的距离是
两点之间的距离是![]() ?
?
(3)若点![]() 沿着
沿着![]() 移动,点
移动,点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 同时出发,点
同时出发,点![]() 从点
从点![]() 移动到点
移动到点![]() 停止时,点
停止时,点![]() 随之也停止移动,试探求经过多长时间△
随之也停止移动,试探求经过多长时间△![]() 的面积为
的面积为![]() 2?
2?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某市区九年级学生每天的健身活动情况,随机从市区九年级的12000名学生中抽取了500名学生,对这些学生每天的健身活动时间进行统计整理,作出了如下不完整的统计图(每组数据含最小值不含最大值,统计数据全部为整数),请根据以下信息解答如下问题:
时间/分 | 频数 | 频率 |
30~40 | 25 | 0.05 |
40~50 | 50 | 0.10 |
50~60 | 75 | b |
60~70 | a | 0.40 |
70~80 | 150 | 0.30 |
(1)a=_______,b=_______;
(2)请补全频数分布直方图;
(3)学生每天健身时间的中位数会落在哪个时间段?
(4)若每天健身时间在60分钟以上为符合每天“阳光一小时”的规定,则符合规定的学生人数大约是多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CF于点F.
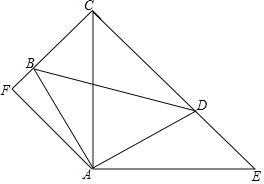
(1)求证:△ABC≌△ADE;
(2)已知BF的长为2,DE的长为6,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产![]() 、
、![]() 两种机械设备,每台
两种机械设备,每台![]() 种设备的成本是
种设备的成本是![]() 种设备的1.5倍,公司若投入16万元生产
种设备的1.5倍,公司若投入16万元生产![]() 种设备,36万元生产
种设备,36万元生产![]() 种设备,则可生产两种设备共10台,请解答下列问题:
种设备,则可生产两种设备共10台,请解答下列问题:
(1)![]() 、
、![]() 两种设备每台的成本分别是多少万元?
两种设备每台的成本分别是多少万元?
(2)![]() 、
、![]() 两种设备每台的售价分别是6万元、10万元,且该公司生产两种设备各30台,现公司决定对两种设备优惠出售,
两种设备每台的售价分别是6万元、10万元,且该公司生产两种设备各30台,现公司决定对两种设备优惠出售,![]() 种设备按原来售价8折出售,B种设备在原来售价的基础上优惠10%,若设备全部售出,该公司一共获利多少万元?
种设备按原来售价8折出售,B种设备在原来售价的基础上优惠10%,若设备全部售出,该公司一共获利多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com