
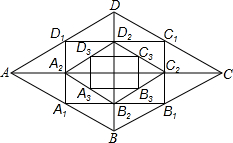
 如图,菱形ABCD的对角线长分别为a、b,以菱形ABCD各边的中点为顶点作矩形A1B1C1D1,然后再以矩形A1B1C1D1的中点为顶点作菱形A2B2C2D2,…,如此下去,得到四边形A2013B2013C2013D2013的面积用含a、b的代数式表示为$\frac{1}{{2}^{2014}}$ab.
如图,菱形ABCD的对角线长分别为a、b,以菱形ABCD各边的中点为顶点作矩形A1B1C1D1,然后再以矩形A1B1C1D1的中点为顶点作菱形A2B2C2D2,…,如此下去,得到四边形A2013B2013C2013D2013的面积用含a、b的代数式表示为$\frac{1}{{2}^{2014}}$ab.  名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 如图,抛物线y=x2+bx-4分别与x轴正半轴、y轴交于点A、B,且$tan∠OBA=\frac{3}{4}$.
如图,抛物线y=x2+bx-4分别与x轴正半轴、y轴交于点A、B,且$tan∠OBA=\frac{3}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
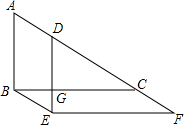 如图,直角三角形△ABC沿着AC所在直线平移得到△DEF,
如图,直角三角形△ABC沿着AC所在直线平移得到△DEF,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知AD是△ABC的中线,AE=EF=FC,下面给出三个关系式:
如图,已知AD是△ABC的中线,AE=EF=FC,下面给出三个关系式:| A. | ①② | B. | ①②③ | C. | ①③ | D. | ②③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com