
【题目】甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:①甲步行的速度为60米/分;②乙走完全程用了30分钟;③乙用12分钟追上甲;④乙到达终点时,甲离终点还有360米;其中正确的结论有( )
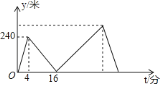
A.1个B.2个C.3个D.4个
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,点P为边AB所在直线上一点,连结CP,M为线段CP的中点,若满足∠ACP=∠MBA,则称点P为△ABC的“好点”.
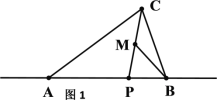
(1)如图2,当∠ABC=90°时,命题“线段AB上不存在“好点”为 (填“真”或“假”)命题,并说明理由;
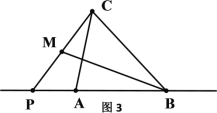
(2)如图3,P是△ABC的BA延长线的一个 “好点”,若PC=4,PB=5,求AP的值;
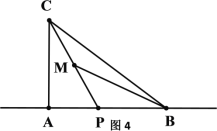
(3)如图4,在Rt△ABC中,∠CAB=90°,点P是△ABC的“好点”,若AC=4,AB=5,求AP的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
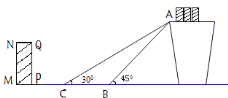
【题目】(本题满分8分)如图是某货站传送货物的平面示意图. 为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°. 已知原传送带AB长为4米.
(1)求新传送带AC的长度;
(2)如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点4米的货物MNQP是否需要挪走,并说明理由.(说明:⑴⑵的计算结果精确到0.1米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24,
≈2.24,![]() ≈2.45)
≈2.45)
查看答案和解析>>
科目:初中数学 来源: 题型:
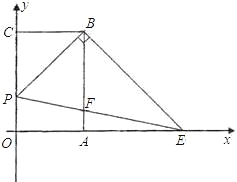
【题目】如图,已知矩形OABC,以点O为坐标原点建立平面直角坐标系,其中A(2,0),C(0,3),点P以每秒1个单位的速度从点C出发在射线CO上运动,连接BP,作BE⊥PB交x轴于点E,连接PE交AB于点F,设运动时间为t秒.
(1)当t=2时,求点E的坐标;
(2)若AB平分∠EBP时,求t的值.
(3)在运动的过程中,是否存在以P、O、E为顶点的三角形与△ABE相似.若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,若BF=12,AB=10,则AE的长为( )
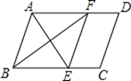
A. 13B. 14C. 15D. 16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,在△ABC中,AB=AC,点 D 是边 BC 的中点.以BD为直径作⊙O,交边 AB于点P,连接PC,交AD于点E.
(1)求证:AD是⊙O的切线;
(2)当∠BAC=90°时,求证:CE=2PE;
(3)如图2,当PC是⊙O的切线,E为AD 中点,BC=8,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,己知点A(8,0),点C(0,6),点B在x轴负半轴上,且AB=AC.
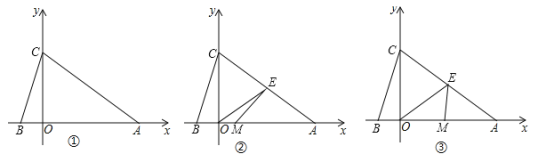
(1)求点B的坐标;
(2)如图2,若点E为边AC的中点,动点M从点B出发以每秒2个单位长度的速度沿线段BA向点A匀速运动,设点M运动的时间为t(秒);
①若△OME的面积为2,求t的值;
②如图3,在点M运动的过程中,△OME能否成为直角三角形?若能,求出此时t的值,并写出相应的点M的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,E是AB延长线上一点,分别以AB、BE为一边在直线AE同侧作正方形ABCD和正方形BEFG,连接AG、CE.

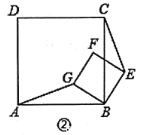
(1)试探究线段AG与CE的大小关系,并证明你的结论;
(2)若AG恰平分∠BAC,且BE=1,试求AB的长;
(3)将正方形BEFG绕点B逆时针旋转一个锐角后,如图②,问(1)中结论是否仍然成立,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com