
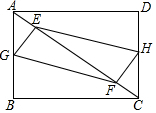
 ��ͼ���ھ���ABCD�У�AB=3cm��BC=4cm��E��F�ǶԽ���AC�ϵ��������㣬�ֱ��A��Cͬʱ����������У��ٶȾ�Ϊ1cm/�룬�˶�ʱ��Ϊt�룬������һ�����㵽����ֹͣ�˶���
��ͼ���ھ���ABCD�У�AB=3cm��BC=4cm��E��F�ǶԽ���AC�ϵ��������㣬�ֱ��A��Cͬʱ����������У��ٶȾ�Ϊ1cm/�룬�˶�ʱ��Ϊt�룬������һ�����㵽����ֹͣ�˶������� ��1���ɡ�����Ա߷ֱ���ȵ��ı�����ƽ���ı��Ρ����ж���
��2���ɡ��Խ�����ȵ�ƽ���ı����Ǿ��Ρ��ж��ı���EGFHΪ����ʱt��ȡֵ��
��3�����ȣ����ı���EGFHΪ����ʱ����Խ����ഹֱ�һ���ƽ�֣��ڸ�����һ�ص㹹��ֱ�������Σ����ù��ɶ������t��ֵ��
��� �⣺��1��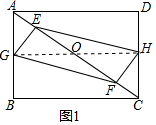 ��ͼ1������GH��AC��O��
��ͼ1������GH��AC��O��
���ı���ABCD�Ǿ��Σ�
��AB=CD��AB��CD��
��G��H�ֱ���AB��DC�е㣬
��AG=$\frac{1}{2}$AB��CH=$\frac{1}{2}$CD��
��AG=CH��
��OG=OH��OA=OC��
������ã�AE=CF��
��OE=OF��
���ı���EGFHʼ����ƽ���ı��Σ�
��2���ߡ�ABC=90�㣬AB=3cm��BC=4cm��
��AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=5��
��G��H�ֱ���AB��DC�е㣬
��GH=BC=4��
���ı���EGFHΪ����ʱ��GH=EF��
��AE=$\frac{1}{2}$��AC-EF��=$\frac{1}{2}$��
��AE=CF=t��EF=5-2��5-t��=4
��ã�t=$\frac{9}{2}$��
�൱�ı���EGFHΪ����ʱ���˶�ʱ��t��ֵΪ$\frac{1}{2}$���$\frac{9}{2}$�룻
��3�����ı���EGFHΪ����ʱ��GH��EF��
���G��H�ֱ���BC��AD�ϣ�
�ߡ�ABC=��GOC=90�㣬��ACB=��GCO��
���COG�ס�CBA��
��$\frac{OG}{AB}$=$\frac{CG}{AC}$����$\frac{OG}{3}$=$\frac{7-t}{5}$��
��ã�OG=$\frac{21-3t}{5}$��
��Rt��ABG��AG2=32+��t-3��2��
��Rt��AOG��AG2=OG2+AO2����32+��t-3��2=��$\frac{21-3t}{5}$��2+$\frac{25}{4}$��
��ã�t=$\frac{31}{8}$��
�ʴ�Ϊ��$\frac{31}{8}$��
���� ���⿼���������ı��ε��ж������ʼ��ۺ�Ӧ�ã�����Ĺؼ����������������ı��ε����ʡ��ж�������Ӧ�ô����ķ�����������������ʶ��


 �ݾ�ѵ������ϵ�д�
�ݾ�ѵ������ϵ�д� С����ȫ�ܼ��ϵ�д�
С����ȫ�ܼ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=3x-1 | B�� | y=-2x | C�� | y=$\frac{1}{x}$ | D�� | y=x2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | Ҫ�˽�һ���ȵ��ݵ�ʹ������ | |
| B�� | Ҫ�˽���ǵ���̨��������š��������� | |
| C�� | Ҫ�˽�ijУ�����12����Ա������״�� | |
| D�� | Ҫ�˽�ȫ������ԡ������������ᡱ������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ab��0 | B�� | a-b��0 | C�� | a+b��0 | D�� | a2+b��0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
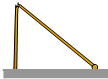 ��ͼ��һ��˱����ζϣ���˵Ķ����ŵص㵽��˵ײ��ľ���Ϊ4m���۶ϵ�����˵ײ��ĸ߶�Ϊ3m������˵ĸ߶�Ϊ8m��
��ͼ��һ��˱����ζϣ���˵Ķ����ŵص㵽��˵ײ��ľ���Ϊ4m���۶ϵ�����˵ײ��ĸ߶�Ϊ3m������˵ĸ߶�Ϊ8m���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
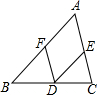 ��ͼ����D��BC�ϣ�DE��AB����AC�ڵ�E��F��AB�ϵ�һ���㣮
��ͼ����D��BC�ϣ�DE��AB����AC�ڵ�E��F��AB�ϵ�һ���㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{18}$=3$\sqrt{2}$ | B�� | $\sqrt{2}$��$\sqrt{3}$=$\sqrt{6}$ | C�� | ��$\sqrt{5}$+1��2=6 | D�� | ��$\sqrt{3}$+2����$\sqrt{3}$-2��=-1 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com