
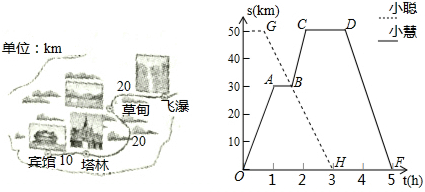
分析 (1)根据时间=路程÷速度,可得小聪骑车从飞瀑出发到宾馆所用时间为:50÷20=2.5(小时),从10点往前推2.5小时,即可解答;
(2)利用得到待定系数法求GH的解析式,当s=30时,求出t的值,即可确定点B的坐标;
(3)根据50÷30=$\frac{5}{3}$(小时)=1小时40分钟,确定当小慧在D点时,对应的时间点是10:20,而小聪到达宾馆返回的时间是10:00,设小聪返回x小时后两人相遇,根据题意得:30x+30(x-$\frac{1}{3}$)=50,解得:x=1,10+1=11点,即可解答.
解答 解:(1)小聪骑车从飞瀑出发到宾馆所用时间为:50÷20=2.5(小时),
∵上午10:00小聪到达宾馆,
∴小聪上午7点30分从飞瀑出发.
(2)3-2.5=0.5,
∴点G的坐标为(0.5,50),
设GH的解析式为s=kt+b,
把G(0.5,50),H(3,0)代入得;$\left\{\begin{array}{l}{0.5k+b=50}\\{3k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-20}\\{b=60}\end{array}\right.$,
∴s=-20t+60,
当s=30时,t=1.5,
∴B点的坐标为(1.5,30),
点B的实际意义是当小慧出发1.5小时时,小慧与小聪相遇,且离宾馆的路程为30km.
(3)50÷30=$\frac{5}{3}$(小时)=1小时40分钟,12-$\frac{5}{3}=10\frac{1}{3}$,
∴当小慧在D点时,对应的时间点是10:20,
而小聪到达宾馆返回的时间是10:00,
设小聪返回x小时后两人相遇,根据题意得:30x+30(x-$\frac{1}{3}$)=50,
解得:x=1,
10+1=11=11点,
∴小聪到达宾馆后,立即以30km/h的速度按原路返回,那么返回途中他11点遇见小慧.
点评 本题考查了一次函数的应用,解决本题的关键是根据题意结合图象说出其图象表示的实际意义,这样便于理解题意及正确的解题.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:解答题
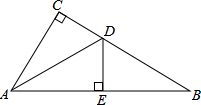
 如图,在△ABC中,AC=BC,∠ACB=90°,延长BC到D,使BD=BA,BE⊥AD于点E,交AC于点F.
如图,在△ABC中,AC=BC,∠ACB=90°,延长BC到D,使BD=BA,BE⊥AD于点E,交AC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①② | C. | ① | D. | ② |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).| 月均用水量(单位:t) | 频数 | 百分比 |
| 2≤x<3 | 2 | 4% |
| 3≤x<4 | 12 | 24% |
| 4≤x<5 | 15 | 30% |
| 5≤x<6 | 10 | 20% |
| 6≤x<7 | 6 | 12% |
| 7≤x<8 | 3 | 6% |
| 8≤x<9 | 2 | 4% |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE⊥AB,垂足为E,DE=1,则BC=( )
如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE⊥AB,垂足为E,DE=1,则BC=( )| A. | $\sqrt{3}$ | B. | 2 | C. | 3 | D. | $\sqrt{3}$+2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com