
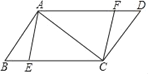
【题目】如图,在平行四边形ABCD中,AB=6,BC=10,对角线AC⊥AB,点E、F分别是BC、AD上的点,且BE=DF.
(1)求证:四边形AECF是平行四边形;
(2)当BE长度为 时,四边形AECF是菱形.
【答案】(1)证明见解析;(2)5.
【解析】
(1)首先根据平行四边形的性质可得AD∥BC,AD=BC,再证明AF=EC,可证明四边形AECF是平行四边形;
(2)由菱形的性质得出AE=CE,得出∠EAC=∠ECA,由角的互余关系证出∠B=∠BAE,得出AE=BE,即可得出结果;
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵BE=DF,
∴AF=EC,
∴四边形AECF是平行四边形;
(2)∵四边形AECF是菱形,
∴AE=CE,
∴∠EAC=∠ECA,
∵AC⊥AB,
∴∠BAC=90°,
∴∠B+∠ECA=90°,∠BAE+∠EAC=90°,
∴∠B=∠BAE,
∴AE=BE,
∴BE=CE=![]() BC=5;
BC=5;
故答案为:5


科目:初中数学 来源: 题型:
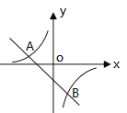
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 图象交于A(-2,1)、B(1,n)两点.
图象交于A(-2,1)、B(1,n)两点.
(1)求反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值大于反比例函数的值的x的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
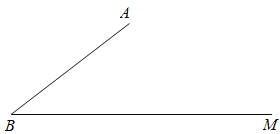
【题目】如图,已知∠ABM=30°,AB=20,C是射线BM上一点.
(1)在下列条件中,可以唯一确定BC长的是 ;(填写所有符合条件的序号)
①AC=13;②tan∠ACB=![]() ;③△ABC的面积为126.
;③△ABC的面积为126.
(2)在(1)的答案中,选择一个作为条件,画出示意图,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是圆O的直径,点C、D在圆O上,且AD平分∠CAB.过点D作AC的垂线,与AC的延长线相交于E,与AB的延长线相交于点F.
求证:EF与圆O相切.

查看答案和解析>>
科目:初中数学 来源: 题型:
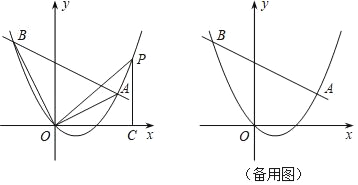
【题目】如图,在平面直角坐标系中,直线y=kx﹣4k+4与抛物线y=![]() x2﹣x交于A、B两点.
x2﹣x交于A、B两点.
(1)直线总经过定点,请直接写出该定点的坐标;
(2)点P在抛物线上,当k=﹣![]() 时,解决下列问题:
时,解决下列问题:
①在直线AB下方的抛物线上求点P,使得△PAB的面积等于20;
②连接OA,OB,OP,作PC⊥x轴于点C,若△POC和△ABO相似,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲地到乙地有两条公路,一条是全长600km的普通公路,另一条是全长480km的高速公路,某客车在高速公路上行驶的平均速度比在普通公路上快45![]() /
/![]() ,由高速公路从甲地到乙地所需的时间是由普通公路从甲地到乙地所需时间的一半,求该客车由高速公路从甲地到乙地所需的时间.
,由高速公路从甲地到乙地所需的时间是由普通公路从甲地到乙地所需时间的一半,求该客车由高速公路从甲地到乙地所需的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种产品形状是长方形,长为8cm,它的展开图如图:
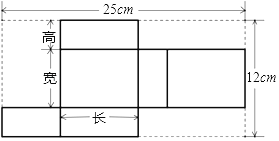
(1)求长方体的体积;
(2)请为厂家设计一种包装纸箱,使每箱能装10件这种产品,要求没有空隙且要使该纸箱所用材料尽可能少(纸箱的表面积尽可能小)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是⊙O 外一点,PA切⊙O于点A,AB是⊙O的直径,连接OP,过点B作BC∥OP交⊙O于点C,连接AC交OP于点D.
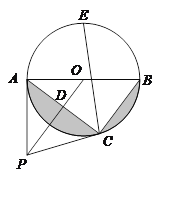
(1)求证:PC是⊙O的切线;
(2)若PD=![]() cm,AC=8cm,求图中阴影部分的面积;
cm,AC=8cm,求图中阴影部分的面积;
(3)在(2)的条件下,若点E是![]() 的中点,连接CE,求CE的长.
的中点,连接CE,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
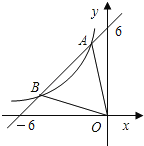
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象相交于A,B两点,且与坐标轴的交点为(﹣6,0),(0,6),点B的横坐标为﹣4.
的图象相交于A,B两点,且与坐标轴的交点为(﹣6,0),(0,6),点B的横坐标为﹣4.
(1)试确定反比例函数的解析式;
(2)求△AOB的面积;
(3)直接写出不等式![]() 的解.
的解.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com