
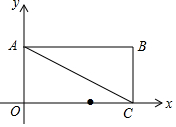
 如图,在平面直角坐标系中,矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=1,OC=2,点D在边OC上且OD=1.25.
如图,在平面直角坐标系中,矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=1,OC=2,点D在边OC上且OD=1.25.分析 (1)先确定A点和C点坐标,然后利用待定系数法求直线AC的解析式;
(2)设M(t,-$\frac{1}{2}$t+1),讨论:当DM=DC时,(t-$\frac{5}{4}$)2+(-$\frac{1}{2}$t+1)2=($\frac{3}{4}$)2,解方程求出t,再求出MD的解析式,从而得到P点坐标;当MD=MC时,易得M点的坐标,接着求出MD的解析式,从而得到P点坐标;当CM=CD时,(t-2)2+(-$\frac{1}{2}$t+1)2=($\frac{3}{4}$)2,解方程求出t,再确定MD的解析式,从而得到P点坐标;
(3),如图2,作O′H⊥x轴于H,则O′D=OD=$\frac{5}{4}$,设O′(m,1),利用勾股定理得的(m-$\frac{5}{4}$)2+12=($\frac{5}{4}$)2,解得m1=2,m2=$\frac{1}{2}$,当m=2时,求出AE长得到E(0,$\frac{5}{2}$),利用待定系数法求出抛物线解析式为y=-(x+$\frac{3}{8}$)2+$\frac{169}{64}$,然后利用抛物线的平移变换求解;当m=$\frac{1}{2}$时,同样可得抛物线解析式为y=-x2+$\frac{3}{4}$x+$\frac{5}{8}$,再利用抛物线的平移变换求解.
解答 解:(1)∵OA=1,OC=2,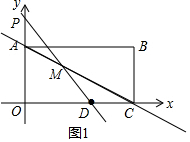
∴A(0,1),C(2,0),
设直线AC的解析式为y=kx+b,
把A(0,1),C(2,0)代入得$\left\{\begin{array}{l}{2k+b=0}\\{b=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=1}\end{array}\right.$,
∴直线AC的解析式为y=-$\frac{1}{2}$x+1;
(2)存在.
D($\frac{5}{4}$,0),CD=2-$\frac{5}{4}$=$\frac{3}{4}$,
设M(t,-$\frac{1}{2}$t+1),
当DM=DC时,(t-$\frac{5}{4}$)2+(-$\frac{1}{2}$t+1)2=($\frac{3}{4}$)2,解得t1=$\frac{4}{5}$,t2=2(舍去),则M($\frac{4}{5}$,$\frac{3}{5}$),此时MD的解析式为y=-$\frac{4}{3}$x+$\frac{5}{3}$,P点坐标为(0,$\frac{5}{3}$);
当MD=MC时,则M点的坐标为($\frac{13}{8}$,$\frac{3}{16}$),此时MD的解析式为y=$\frac{1}{2}$x-$\frac{5}{8}$,P点坐标为(0,-$\frac{5}{8}$);
当CM=CD时,(t-2)2+(-$\frac{1}{2}$t+1)2=($\frac{3}{4}$)2,解得t1=$\frac{20+3\sqrt{5}}{10}$,t2=$\frac{20-3\sqrt{5}}{10}$,
则M($\frac{20+3\sqrt{5}}{10}$,-$\frac{3\sqrt{5}}{20}$)或($\frac{20-3\sqrt{5}}{10}$,$\frac{3\sqrt{5}}{20}$),
此时MD的解析式为y=-($\sqrt{5}$-2)x+$\frac{5(\sqrt{5}-2)}{4}$或y=($\sqrt{5}$+2)x-$\frac{5(\sqrt{5}+2)}{4}$,P点坐标为(0,$\frac{5\sqrt{5}-10}{4}$)或(0,$\frac{-5\sqrt{5}-10}{4}$),
综上所述,P点坐标为(0,$\frac{5}{3}$)或(0,-$\frac{5}{8}$)或(0,$\frac{5\sqrt{5}-10}{4}$)或(0,$\frac{-5\sqrt{5}-10}{4}$);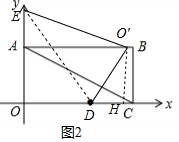
(3)△ODE沿DE折叠后点O落在边AB上O′处,如图2,作O′H⊥x轴于H,则O′D=OD=$\frac{5}{4}$,
设O′(m,1),
在Rt△O′DH中,(m-$\frac{5}{4}$)2+12=($\frac{5}{4}$)2,解得m1=2,m2=$\frac{1}{2}$,
当m=2时,AO′=2,而EO′=EO=EA+1,
∴EA2+22=(EA+1)2,解得EA=$\frac{3}{2}$,
∴E(0,$\frac{5}{2}$),
设平移的抛物线解析式为y=-x2+bx+c,
把E(0,$\frac{5}{2}$),D($\frac{5}{4}$,0)代入得$\left\{\begin{array}{l}{c=\frac{5}{2}}\\{-\frac{25}{16}+\frac{5}{4}b+c=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=-\frac{3}{4}}\\{c=\frac{5}{2}}\end{array}\right.$,
∴抛物线解析式为y=-x2-$\frac{3}{4}$x+$\frac{5}{2}$,
∵y=-(x+$\frac{3}{8}$)2+$\frac{169}{64}$,
∴抛物线y=-x2先向左$\frac{3}{8}$单位,再向上平移$\frac{169}{64}$单位,才能使得平移后的抛物线过点D和点E;
当m=$\frac{1}{2}$时,AO′=$\frac{1}{2}$,而EO′=EO=1-AE,
∴EA2+($\frac{1}{2}$)2=(1-AE)2,解得EA=$\frac{3}{8}$,
∴E(0,$\frac{5}{8}$),
同样可得抛物线解析式为y=-x2+$\frac{3}{4}$x+$\frac{5}{8}$,
∵y=-(x-$\frac{3}{8}$)2+$\frac{49}{64}$,
∴抛物线y=-x2先向右$\frac{3}{8}$单位,再向上平移$\frac{49}{64}$单位,才能使得平移后的抛物线过点D和点E.
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象的平移变换和矩形的性质、折叠的性质和等腰三角形的判定;会运用待定系数法求一次函数和二次函数的解析式;会运用勾股定理和两点间的距离公式计算线段的长;理解坐标与图形的性质;注意分类讨论思想的应用.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
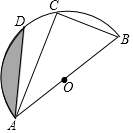 已知:如图,AB为半圆O的直径,C、D是半圆O上的两点,若直径AB的长为12,且BC=6,∠DAB=45°.(1)求∠DAC的度数;(2)求图中阴影部分的面积(结果保留π).
已知:如图,AB为半圆O的直径,C、D是半圆O上的两点,若直径AB的长为12,且BC=6,∠DAB=45°.(1)求∠DAC的度数;(2)求图中阴影部分的面积(结果保留π).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
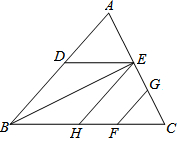 请将下列证明过程补充完整:如图,在△ABC中,DE∥BC,GF∥AB,∠ABC=∠DEH,求证:GF∥EH.
请将下列证明过程补充完整:如图,在△ABC中,DE∥BC,GF∥AB,∠ABC=∠DEH,求证:GF∥EH.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com