解:(1)连接MM′、NN′.
∵DE和BC是⊙O
1的切线,DE∥BC,
∴MM′过点O
1.同理NN'过点O
2.∵MM′⊥BC,MM′⊥DE,NN′⊥BC
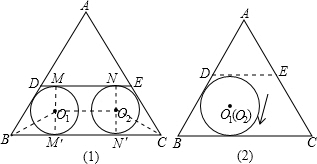
∴四边形MM′N′N是矩形.
∴MM′=NN′,即⊙O
1和⊙O
2是等圆;
(2)连接O
lB,O
lO
2,O
2C,O
lM′,O
2N′.
易证四边形O
1BCO
2是等腰梯形,四边形O
1M′N′O
2是矩形.
在Rt△O
1BM′中,∠0
1BM′=30°,O
lM′=x,
则BM′=

x.
∵y=O
10
2=M′N′,BM′=N′C=

x,BC=BM′+M′N′+N′C,
∴y+2

=a,
∴y=a-2

x,
求得0<x≤
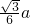
;
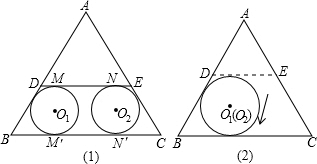
(3)当⊙O
l和⊙O
2外切时,O
lO
2=2x,2x=a-2

x,
∴x=(

-1)

;
(4)当DE是△ABC的中位线时,求得x=

.
此时BM'=

x=

a.
⊙O
1的圆心O
1所经过的路线是与△ABC相似,且各边与△ABC各边距离为

的正三角形.
其边长为a-

a×2=

,
∴所求的圆心O
1走过的长度为:

×3=

a.
分析:(1)根据连接圆的两条平行切线的切点的线段是直径,以及切线的性质判定四边形是矩形,再根据矩形的性质即可证明;
(2)根据30°的直角三角形的性质,分别用圆的半径表示出BM′和CN′的长,即可写出y与x的函数关系式;根据y=0,即可求得x的最大值;
(3)根据两圆外切,圆心距等于两圆半径之和,再结合(2)中的函数关系式求得x的值;
(4)首先根据等边三角形的高,结合三角形的中位线定理求得x的值;
再根据⊙O
1的圆心O
1所经过的路线,是与△ABC相似,且各边与△ABC各边距离为

的正三角形.
结合等边三角形的性质进行计算.
点评:综合运用了等边三角形的性质、矩形的判定和性质以及两圆的位置关系和数量之间的联系.


 x.
x. x,BC=BM′+M′N′+N′C,
x,BC=BM′+M′N′+N′C, =a,
=a, x,
x,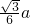 ;
; x,
x, -1)
-1) ;
; .
. x=
x= a.
a. 的正三角形.
的正三角形. a×2=
a×2= ,
, ×3=
×3= a.
a. 的正三角形.
的正三角形.

 阅读快车系列答案
阅读快车系列答案
