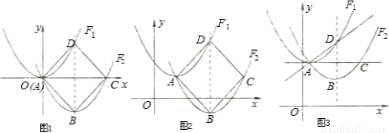
解:(1)由F
1:y=

x
2,平移后得到F
2,使得四边形ABCD为正方形,可以得出F
2的顶点坐标为(a,-a),D点的坐标为(b,b),
b=

b
2,
解得:b=0或3,0不合题意舍去,
故:D(3,3),F
2的顶点坐标为(a,-a),代入y=

(x-a)
2-a,
解得:F
2的顶点坐标为(3,-3),
∴y=

(x-3)
2-3,
(2)∵设F
1顶点坐标为A(m,n),平移距离为t,则C点坐标:C(m+2t,n).
平移之后的解析式:F
1顶点A坐标为A(m,n),
所以F
1可以表示为y=a(x-m)
2+n,
则平移之后的解析式为y=a(x-m-t)
2+n-t ①
将C点坐标代入①式,得到n=at
2+n-t,
即at
2-t=0,所以t=

∴正方形面积=2t
2=

;
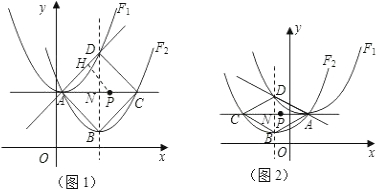
(3)当点C在点A的右侧时(如图1),
设AC与BD交于点N,
抛物线y=

x
2-

x+

,配方得y=

(x-1)
2+2,
其顶点坐标是A(1,2),
∵AC=2

,
∴点C的坐标为(1+2

,2).
∵F
2过点A,
∴F
2解析式为y=

(x-1-

)
2+1,
∴B(1+

,1),
∴D(1+

,3)
∴NB=ND=1,
∵点A与点C关于直线BD对称,
∴AC⊥DB,且AN=NC
∴四边形ABCD是菱形.
∴PD=PB.
作PH⊥AD交AD于点H,则PD+PH=PB+PH.
要使PD+PH最小,即要使PB+PH最小,
此最小值是点B到AD的距离,即△ABD边AD上的高h.
∵DN=1,AN=

,DB⊥AC,
∴∠DAN=30°,
故△ABD是等边三角形.
∴h=

AD=

∴最小值为

.
当点C在点A的左侧时(如图2),同理,最小值为

.
综上,点P到点D的距离和到直线AD的距离之和的最小值为

.
分析:(1)由F
1:y=

x
2,平移后得到F
2,使得四边形ABCD为正方形,可以得出F
2的顶点坐标为(a,-a),D点的坐标为(b,b),进而求出已知坐标,即可得出a,b的值,进而求出F
2的解析式;
(2)设F1顶点坐标为A(m,n),平移距离为t,则C点坐标:C(m+2t,n),求出平移之后的解析式,进而得出t的值,从而求出正方形面积;
(3)要分情况讨论点C在点A的左边还是右边,作PH⊥AD交AD于点H,则PD+PH=PB+PH,是PB+PH值最小可求出h的最小值.
点评:此题主要考查了考生的作图能力以及二次函数的平移的性质和正方形的性质等知识,此题难度较大,灵活运用二次函数与正方形性质是解决问题的关键.

 x2,平移后得到F2,使得四边形ABCD为正方形,求F2的解析式;
x2,平移后得到F2,使得四边形ABCD为正方形,求F2的解析式; x2”改为“y=ax2+bx+c”,其余条件不变,求正方形ABCD的面积(用含有a的代数式表示);
x2”改为“y=ax2+bx+c”,其余条件不变,求正方形ABCD的面积(用含有a的代数式表示); x2”改为“y=
x2”改为“y= x2-
x2- x+
x+ ”,“正方形ABCD”改为“AC=2
”,“正方形ABCD”改为“AC=2 ,且点P是直线AC上的动点”,求点P到真线AD的距离与到点D的距离之和的最小值.
,且点P是直线AC上的动点”,求点P到真线AD的距离与到点D的距离之和的最小值.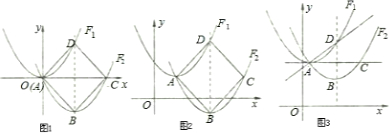
 x2,平移后得到F2,使得四边形ABCD为正方形,可以得出F2的顶点坐标为(a,-a),D点的坐标为(b,b),
x2,平移后得到F2,使得四边形ABCD为正方形,可以得出F2的顶点坐标为(a,-a),D点的坐标为(b,b), b2,
b2, (x-a) 2-a,
(x-a) 2-a, (x-3)2-3,
(x-3)2-3,
 ;
; x2-
x2- x+
x+ ,配方得y=
,配方得y= (x-1)2+2,
(x-1)2+2, ,
, ,2).
,2). (x-1-
(x-1- )2+1,
)2+1, ,1),
,1), ,3)
,3) ,DB⊥AC,
,DB⊥AC, AD=
AD=
 .
. .
. .
.
 x2,平移后得到F2,使得四边形ABCD为正方形,可以得出F2的顶点坐标为(a,-a),D点的坐标为(b,b),进而求出已知坐标,即可得出a,b的值,进而求出F2的解析式;
x2,平移后得到F2,使得四边形ABCD为正方形,可以得出F2的顶点坐标为(a,-a),D点的坐标为(b,b),进而求出已知坐标,即可得出a,b的值,进而求出F2的解析式;

 发散思维新课堂系列答案
发散思维新课堂系列答案
 x2,平移后得到F2,使得四边形ABCD为正方形,求F2的解析式;
x2,平移后得到F2,使得四边形ABCD为正方形,求F2的解析式; x2”改为“y=ax2+bx+c”,其余条件不变,求正方形ABCD的面积(用含有a的代数式表示);
x2”改为“y=ax2+bx+c”,其余条件不变,求正方形ABCD的面积(用含有a的代数式表示); x2”改为“y=
x2”改为“y= x2-
x2- x+
x+ ”,“正方形ABCD”改为“AC=2
”,“正方形ABCD”改为“AC=2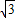 ,且点P是直线AC上的动点”,求点P到真线AD的距离与到点D的距离之和的最小值.
,且点P是直线AC上的动点”,求点P到真线AD的距离与到点D的距离之和的最小值.