
分析 (1)由方程有两个相等的实数根结合根的判别式,即可得出△=8m-4=0,解之即可得出结论;
(2)将m的值代入原方程,利用配方法解方程即可得出结论.
解答 解:(1)∵关于x的一元二次方程x2-2mx+(m-1)2=0有两个相等的实数根,
∴△=(-2m)2-4(m-1)2=8m-4=0,
解得:m=$\frac{1}{2}$.
(2)将m=$\frac{1}{2}$代入原方程得x2-x+$\frac{1}{4}$=(x-$\frac{1}{2}$)2=0,
解得:x1=x2=$\frac{1}{2}$.
点评 本题考查了根的判别式以及配方法解一元二次方程,解题的关键是:(1)牢记“当△=0时,方程有两个相等的实数根”;(2)代入m的值,再解一元二次方程.


科目:初中数学 来源: 题型:填空题
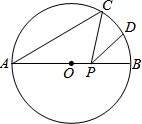 如图,AB是⊙O的直径,AB=10,∠A=40°,点D为弧BC的中点,点P是直径AB上的一个动点,PC+PD的最小值为5$\sqrt{3}$.
如图,AB是⊙O的直径,AB=10,∠A=40°,点D为弧BC的中点,点P是直径AB上的一个动点,PC+PD的最小值为5$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
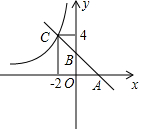 如图,一条直线分别交x轴、y轴于A、B两点,交反比例函数y=$\frac{m}{x}$(m≠0)位于第二象限的一支于C点,OA=OB=2.
如图,一条直线分别交x轴、y轴于A、B两点,交反比例函数y=$\frac{m}{x}$(m≠0)位于第二象限的一支于C点,OA=OB=2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com