
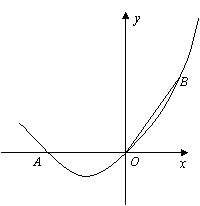
如图,在直角坐标系中,点A的坐标为(-2,0),连结OA,将线段OA绕原点O顺时针旋转120°,得到线段OB.
(1)求点B的坐标;
(2)求经过A、O、B三点的抛物线的解析式;
(3)在(2)中抛物线的对称轴上是否存在点C,使△BOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由.
(4)如果点P是(2)中的抛物线上的动点,且在x轴的下方,那么△PAB是否有最大面积?若有,求出此时P点的坐标及△PAB的最大面积;若没有,请说明理由.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
成都市为了解决街道路面问题,需在中心城区重新铺设一条长3000米的路面,实施施工时“……”,设实际每天铺设路面 米,则可得方程
米,则可得方程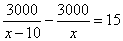 ,根据此情景,题中用“……” 表示的缺失的条件应补为( )
,根据此情景,题中用“……” 表示的缺失的条件应补为( )
A. 每天比原计划多铺设10米,结果延期15天才完成;
B. 每天比原计划少铺设10米,结果延期15天才完成;
C. 每天比原计划多铺设10米,结果提前15天才完成;
D. 每天比原计划少铺设10米,结果提前15天才完成;
查看答案和解析>>
科目:初中数学 来源: 题型:
观察计算
当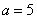 ,
,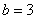 时,
时, 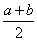 与
与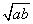 的大小关系是_________________.
的大小关系是_________________.
当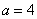 ,
,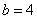 时,
时, 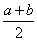 与
与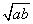 的大小关系是_
的大小关系是_ ________________.
________________.
探究证明
如图所示,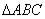 为圆O的内接三角形,
为圆O的内接三角形,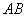 为直径,过C作
为直径,过C作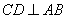 于D,设
于D,设 ,BD=b.
,BD=b.
(1)分别用 表示线段OC,CD;
表示线段OC,CD;
(2)探求OC与CD表达式之间存在的关系(用含a,b的式子表示).
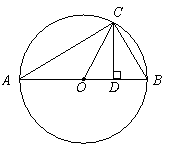
归纳结论
根据上面的观察计算、探究证 明,
明, 你能得出
你能得出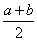 与
与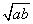 的大小关系是:______________.
的大小关系是:______________.
实践应用
要制作面积为4平方米的长方形镜框,直接利用探究得出的结论,求出镜框周长的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com