
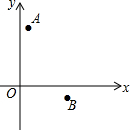 如图,在平面直角坐标系中,点A(1,5),B(3,-1),点M在x轴上,当AM-BM最大时,求点M的坐标.
如图,在平面直角坐标系中,点A(1,5),B(3,-1),点M在x轴上,当AM-BM最大时,求点M的坐标. 分析 作点B关于x轴的对称点B′,连接AB′并延长与x轴的交点,即为所求的M点.利用待定系数法求出直线AB′的解析式,然后求出其与x轴交点的坐标,即M点的坐标.
解答 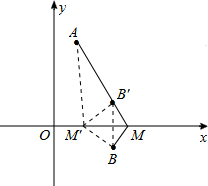 解:如图,作点B关于x轴的对称点B′,连接AB′并延长与x轴的交点,即为所求的M点.此时AM-BM=AM-B′M=AB′.
解:如图,作点B关于x轴的对称点B′,连接AB′并延长与x轴的交点,即为所求的M点.此时AM-BM=AM-B′M=AB′.
不妨在x轴上任取一个另一点M′,连接M′A、M′B、M′B′.
则M′A-M′B=M′A-M′B′<AB′(三角形两边之差小于第三边).
∴M′A-M′B<AM-BM,即此时AM-BM最大.
∵B′是B(3,-1)关于x轴的对称点,
∴B′(3,1).
设直线AB′解析式为y=kx+b,把A(1,5)和B′(3,1)代入得:
$\left\{\begin{array}{l}{k+b=5}\\{3k+b=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-2}\\{b=7}\end{array}\right.$,
∴直线AB′解析式为y=-2x+7.
令y=0,解得x=$\frac{7}{2}$,
∴M点坐标为($\frac{7}{2}$,0).
点评 本题考查了轴对称--最短路线问题、坐标与图形性质.解题时可能感觉无从下手,主要原因是平时习惯了线段之和最小的问题,突然碰到线段之差最大的问题感觉一筹莫展.其实两类问题本质上是相通的,前者是通过对称转化为“两点之间线段最短”问题,而后者(本题)是通过对称转化为“三角形两边之差小于第三边”问题.可见学习知识要活学活用,灵活变通.


科目:初中数学 来源: 题型:解答题
 如图,在等腰直角三角形ABC中,∠ACB=90°,AB=8$\sqrt{2}$cm,点P(不与A,B重合)从点A出发,沿AB方向以$\sqrt{2}$cm/s的速度向终点B运动,在运动过程中,过点P作PQ⊥AB交射线BC于点Q,以线段PQ为边作等腰直角三角形PQR,且∠PQR=90°(点B,R位于PQ两侧),设△PQR与△ABC重叠部分图形的面积为S(cm2),点P的运动时间为t(s).
如图,在等腰直角三角形ABC中,∠ACB=90°,AB=8$\sqrt{2}$cm,点P(不与A,B重合)从点A出发,沿AB方向以$\sqrt{2}$cm/s的速度向终点B运动,在运动过程中,过点P作PQ⊥AB交射线BC于点Q,以线段PQ为边作等腰直角三角形PQR,且∠PQR=90°(点B,R位于PQ两侧),设△PQR与△ABC重叠部分图形的面积为S(cm2),点P的运动时间为t(s).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,矩形ABCD中,BC=2AB,对角线相交于O,过C点作CE⊥BD交BD于E点,H为BC中点,连接AH交BD于G点,交EC的延长线于F点,下列5个结论:①EH=AB;②∠ABG=∠HEC;③△ABG≌△HEC;④S△GAD=S四边形GHCE,⑤CF=BD.正确的有( )个.
如图,矩形ABCD中,BC=2AB,对角线相交于O,过C点作CE⊥BD交BD于E点,H为BC中点,连接AH交BD于G点,交EC的延长线于F点,下列5个结论:①EH=AB;②∠ABG=∠HEC;③△ABG≌△HEC;④S△GAD=S四边形GHCE,⑤CF=BD.正确的有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知?ABCD的对角线AC与BD交于点O,下列结论不正确的是( )
已知?ABCD的对角线AC与BD交于点O,下列结论不正确的是( )| A. | 当AB=BC时,?ABCD是菱形 | B. | 当AC⊥BD时,?ABCD是菱形 | ||
| C. | 当OA=OB时,?ABCD是矩形 | D. | 当∠ABD=∠CBD时,?ABCD是矩形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.1×103 | B. | 1.1×104 | C. | 11×103 | D. | 0.11×105 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com