
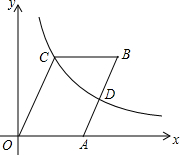
 如图,?OABC的顶点B、C在第一象限,点A的坐标为(3,0),D为边AB的中点,反比例函数y=$\frac{k}{x}$(k>0)的图象经过点C、D两点,若∠COA=60°,则k的值为4$\sqrt{3}$.
如图,?OABC的顶点B、C在第一象限,点A的坐标为(3,0),D为边AB的中点,反比例函数y=$\frac{k}{x}$(k>0)的图象经过点C、D两点,若∠COA=60°,则k的值为4$\sqrt{3}$. 分析 作CE⊥x轴于点E,则∠CEO=90°,过B作BF⊥x轴于F,过D作DM⊥x轴于M,设C的坐标为(x,$\sqrt{3}$x),表示出D的坐标,代入反比例函数的解析式,求出k即可.
解答 解:作CE⊥x轴于点E,则∠CEO=90°,过B作BF⊥x轴于F,过D作DM⊥x轴于M,
则BF=CE,DM∥BF,BF=CE,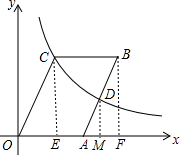
∵D为AB的中点,
∴AM=FM,
∴DM=$\frac{1}{2}$BF,
∵∠COA=60°,
∴∠OCE=30°,
∴OC=2OE,CE=$\sqrt{3}$OE,
∴设C的坐标为(x,$\sqrt{3}$x),
∴AF=OE=x,CE=BF=$\sqrt{3}$x,OE=AF=x,DM=$\frac{\sqrt{3}}{2}$x,
∵四边形OABC是平行四边形,A(3,0),
∴OF=3+x,OM=3+$\frac{1}{2}$x,
即D点的坐标为(3+$\frac{1}{2}$x,$\frac{\sqrt{3}}{2}$x),
把C和D的坐标代入y=$\frac{k}{x}$得:k=x•$\sqrt{3}$x,k=(3+$\frac{1}{2}$x)•$\frac{\sqrt{3}}{2}$x,
解得:x=0或2(x=0不符合题意舍去),
k=4$\sqrt{3}$,
故答案为:4$\sqrt{3}$.
点评 本题考查了平行四边形的性质,待定系数法求函数的解析式,解直角三角形的应用,能得出关于x、k的方程是解此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
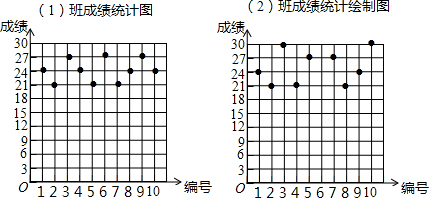
| 班级 | 平均数(分) | 中位数(分) | 众数(分) |
| (1)班 | 24 | 24 | 24 |
| (2)班 | 24 | 24 | 21 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
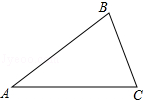 已知:在△ABC中,AB=AC.
已知:在△ABC中,AB=AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
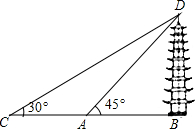 五一节,某校数学兴趣小组的同学相约去东台西溪“海春轩塔”参观,并测量其高度.如图,塔身BD与地面垂直,他们先在A处测得塔顶端点D的仰角为45°,再沿着BA的方向后退16cm至C处,测得塔顶端点D的仰角为30°,求“海春轩塔”BD的高度.($\sqrt{3}$≈1.73,结果保留一位小数)
五一节,某校数学兴趣小组的同学相约去东台西溪“海春轩塔”参观,并测量其高度.如图,塔身BD与地面垂直,他们先在A处测得塔顶端点D的仰角为45°,再沿着BA的方向后退16cm至C处,测得塔顶端点D的仰角为30°,求“海春轩塔”BD的高度.($\sqrt{3}$≈1.73,结果保留一位小数)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
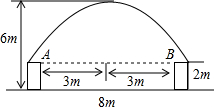 某一隧道内设双行线公路,其截面由一长方形和一抛物线构成,如图所示,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5m,若行车道总宽度AB为6m,请计算车辆经过隧道时的限制高度是多少米?(精确到0.1m)
某一隧道内设双行线公路,其截面由一长方形和一抛物线构成,如图所示,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5m,若行车道总宽度AB为6m,请计算车辆经过隧道时的限制高度是多少米?(精确到0.1m)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com