
(本题满分12分)有一批图形计算器,原售价为每台800元,在甲、乙两家公司销售.甲公司用如下方法促销:买一台单价为780元,买两台每台都为760元.依此类推,即每多买一台则所买各台单价均再减20元,但最低不能低于每台440元;乙公司一律按原售价的75%促销.某单位需购买一批图形计算器:
1.(1)若此单位需购买6台图形计算器,应去哪家公司购买花费较少?
2.(2)若此单位恰好花费7 500元,在同一家公司购买了一定数量的图形计算器,请问是在哪家公司购买的,数量是多少?
科目:初中数学 来源:2011-2012学年江苏省苏州市九年级10月月考数学卷 题型:解答题
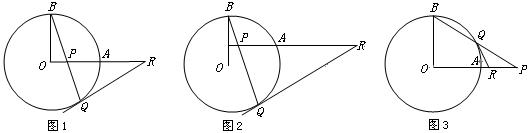
(本题满分12分)有这样一道习题:已知:如图1,OA和OB是⊙O的半径,并且OA⊥OB,P是OA上任一点(不与O、A重合),BP的延长线交⊙O于Q,R是OA的延长线上一点,且RP=RQ.说明:RQ为⊙O的切线. (无须证明)
请探究下列变化:
变化一:交换题设与结论.
如图1,已知OA和OB是⊙O的半径,并且OA⊥OB,P是OA上任一点(不与O、A重合),BP的延长线交⊙O于Q,过Q点作⊙O的切线交OA的延长线于R.说明:RP=RQ.(要证明)

变化二:运动探求.
(1)如图2,若OA向上平移,变化一中的结论还成立吗?(只需交待判断) 答:_________.
(2)如图3,如果P在OA的延长线上时,BP交⊙O于Q,过点Q作⊙O的切线交OA的延长线于R,变化一中的结论还成立吗?为什么? 来]
查看答案和解析>>
科目:初中数学 来源:2011年江苏省苏州市中考模拟(二)数学卷 题型:解答题
(本题满分12分)在四边形ABCD中,AD=a,CD=b,点E在射线BA上,点F在射线BC上.
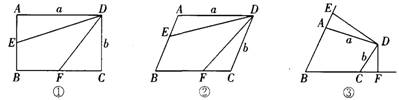
观察计算:
(1)如图①,若四边形ABCD是矩形,E是AB的中点.F是BC的中点,则四边形DEBF 的面积S四边形DEBF=_______.
(2)若四边形ABCD是平行四边形,E是AB的中点,F是BC的中点,则S四边形DEBF:S四边形ABCD=_______.
(3)如图②,若四边形ABCD是平行四边形,且BE:AB=2:3,BF:BC=2:3,则S四边形DEBF:S四边形ABCD=_______.
探索规律:
如图③,在四边形ABCD中,若BE:AB=n:m,BF:BC=n:m,试猜想S四边形DEBF:S四边形ABCD=_______,请说明理由.
解决问题:
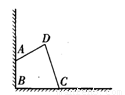
如图④,某小区角落有一四边形空地,为了充分利用空间,美化环境,想把它沿两侧墙壁改造为一块绿地,使绿地面积是原空地面积的3倍.请分别在两侧墙壁上确定点E、F,画出改造线DE、DF,并写出作法.
查看答案和解析>>
科目:初中数学 来源: 题型:
(本题满分12分)有这样一道习题:已知:如图1,OA和OB是⊙O的半径,并且OA⊥OB,P是OA上任一点(不与O、A重合),BP的延长线交⊙O于Q,R是OA的延长线上一点,且RP=RQ.说明:RQ为⊙O的切线. (无须证明)
请探究下列变化:
变化一:交换题设与结论.
如图1,已知OA和OB是⊙O的半径,并且OA⊥OB,P是OA上任一点(不与O、A重合),BP的延长线交⊙O于Q,过Q点作⊙O的切线交OA的延长线于R.说明:RP=RQ.(要证明)
变化二:运动探求.
(1)如图2,若OA向上平移,变化一中的结论还成立吗?(只需交待判断) 答:_________.
(2)如图3,如果P在OA的延长线上时,BP交⊙O于Q,过点Q作⊙O的切线交OA的延长线于R,变化一中的结论还成立吗?为什么? 来]
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2012届江苏省苏州市相城实验中学九年级10月月考数学卷 题型:解答题
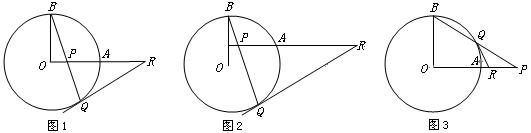
(本题满分12分)有这样一道习题:已知:如图1,OA和OB是⊙O的半径,并且OA⊥OB,P是OA上任一点(不与O、A重合),BP的延长线交⊙O于Q,R是OA的延长线上一点,且RP=RQ.说明:RQ为⊙O的切线. (无须证明)
请探究下列变化:
变化一:交换题设与结论.
如图1,已知OA和OB是⊙O的半径,并且OA⊥OB,P是OA上任一点(不与O、A重合),BP的延长线交⊙O于Q,过Q点作⊙O的切线 交OA的延长线于R.说明:RP=RQ.(要证明)
交OA的延长线于R.说明:RP=RQ.(要证明)
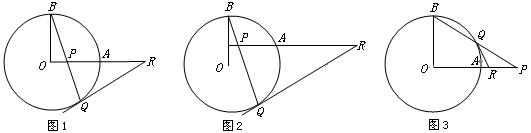
变化二:运动探求.
(1)如图2,若OA向上平移,变化一中的结论还成立吗?(只需交待判断) 答:_________ .
.
(2)如图3,如果P在OA的延长线上时,BP交⊙O于Q,过点Q作⊙O的切线交OA的延长线于R,变化一中的结论还成立吗?为什么? 来]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com