Question

15．如图1，在△ABC中，AC=BC，点E为AB边上的一动点，过点E作AB垂线交AC或BC于点D．点P为BA延长线上一点，且BA=2PA，连接PD，直线PD交CE于点F，其中AE=nBE．

（1）如图1，若n=3，则$\frac{EF}{FC}$=$\frac{5}{6}$；
（2）如图2，当0＜n＜1时，求$\frac{EF}{FC}$的值；
（3）若$\frac{EF}{FC}$=2，请直接写出n的值．

Answer 1

分析 解：（1）设BE=a，则AE=3a，BA=4a，PA=2a，作AQ⊥AB交PD于Q，作CM⊥AB于M，由等腰三角形的性质得出AM=BM=$\frac{1}{2}$BA=2a=PA，得出PE=5a，设AQ=b，由DE∥CM∥AQ，得出Q为PN的中点，△PDE∽△PQA，△DEF∽△NCF，由三角形中位线定理得出MN=2AQ=2b，由相似三角形的性质得出$\frac{DE}{AQ}=\frac{PE}{PA}$=$\frac{5a}{2a}$=$\frac{5}{2}$，$\frac{EF}{FC}=\frac{DE}{CN}$，得出DE=$\frac{5}{2}$AQ=$\frac{5}{2}$b，由三角形中位线定理得出CM=2DE=5b，求出CN=CM-MN=3b，即可得出结果；
（2）设BE=a，则AE=na，BA=a+na，PA=$\frac{1+n}{2}$a，作AQ⊥AB交PD于Q，作CM⊥AB于M，由等腰三角形的性质得出AM=BM=$\frac{1}{2}$BA=$\frac{1+n}{2}$a=PA，得出PE=$\frac{3n+1}{2}$a，设AQ=b，由DE∥CM∥AQ，得出Q为PN的中点，△PDE∽△PQA，△DEF∽△NCF，△ACM∽△ADE，得出MN=2AQ=2b，$\frac{DE}{AQ}=\frac{PE}{PA}$=$\frac{3n+1}{n+1}$，$\frac{EF}{FC}=\frac{DE}{CN}$，$\frac{CM}{DE}=\frac{AM}{AE}$=$\frac{n+1}{2n}$，求出DE=$\frac{3n+1}{n+1}$b，CM=$\frac{3n+1}{2n}$b，得出CN=CM-MN=$\frac{1-n}{2n}$b，即可得出结果；
（3）分两种情况：①当0＜n＜1时，由已知条件得出方程，解方程即可；②当n＞1时，同（2）得：$\frac{EF}{FC}=\frac{6n+2}{3（{n}^{2}-1）}$，得出方程$\frac{6n+2}{3（{n}^{2}-1）}$=2，解方程即可．

解答 解：（1）设BE=a，则AE=3a，BA=4a，
∵BA=2PA，
∴PA=2a，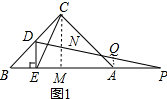
作AQ⊥AB交PD于Q，作CM⊥AB于M，如图1所示：
∵AC=BC，
∴AM=BM=$\frac{1}{2}$BA=2a=PA，
∴PE=5a，
设AQ=b，
∵DE⊥AB，
∴DE∥CM∥AQ，
∴Q为PN的中点，△PDE∽△PQA，△DEF∽△NCF，
∴MN=2AQ=2b，$\frac{DE}{AQ}=\frac{PE}{PA}$=$\frac{5a}{2a}$=$\frac{5}{2}$，$\frac{EF}{FC}=\frac{DE}{CN}$，
∴DE=$\frac{5}{2}$AQ=$\frac{5}{2}$b，
∵BE=ME=a，DE∥CM，
∴DE是△BCM的中位线，
∴CM=2DE=5b，
∴CN=CM-MN=5b-2b=3b，
∴$\frac{EF}{FC}$=$\frac{\frac{5}{2}b}{3b}$=$\frac{5}{6}$，
故答案为：$\frac{5}{6}$；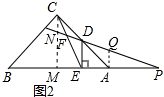
（2）同（1），设BE=a，则AE=na，BA=a+na，
∵BA=2PA，
∴PA=$\frac{1+n}{2}$a，
作AQ⊥AB交PD于Q，作CM⊥AB于M，如图2所示：
∵AC=BC，
∴AM=BM=$\frac{1}{2}$BA=$\frac{1+n}{2}$a=PA，
∴PE=$\frac{3n+1}{2}$a，
设AQ=b，
∵DE⊥AB，
∴DE∥CM∥AQ，
∴Q为PN的中点，△PDE∽△PQA，△DEF∽△NCF，△ACM∽△ADE，
∴MN=2AQ=2b，$\frac{DE}{AQ}=\frac{PE}{PA}$=$\frac{\frac{3n+1}{2}a}{\frac{1+n}{2}a}$=$\frac{3n+1}{n+1}$，$\frac{EF}{FC}=\frac{DE}{CN}$，$\frac{CM}{DE}=\frac{AM}{AE}$=$\frac{\frac{1+n}{2}a}{na}$=$\frac{n+1}{2n}$，
∴DE=$\frac{3n+1}{n+1}$b，CM=$\frac{3n+1}{2n}$b，
∴CN=CM-MN=$\frac{1-n}{2n}$b，
∴$\frac{EF}{FC}=\frac{DE}{CN}$=$\frac{\frac{3n-1}{n+1}}{\frac{1-n}{2n}}$=$\frac{6{n}^{2}+2n}{1-{n}^{2}}$；
（3）分两种情况：
①当0＜n＜1时，由（2）得：$\frac{6{n}^{2}+2n}{1-{n}^{2}}$=2，
解得：n=$\frac{-1±\sqrt{17}}{8}$（负值舍去），
∴n=$\frac{1+\sqrt{17}}{8}$；
②当n＞1时，同（2）得：$\frac{EF}{FC}=\frac{6n+2}{3（{n}^{2}-1）}$，
∴$\frac{6n+2}{3（{n}^{2}-1）}$=2，
解得：n=$\frac{3±\sqrt{57}}{6}$（负值舍去），
∴n=$\frac{3+\sqrt{57}}{6}$；
综上所述：若$\frac{EF}{FC}$=2，n的值为$\frac{1+\sqrt{17}}{8}$或$\frac{3+\sqrt{57}}{6}$．

点评 本题是相似形综合题目，考查了相似三角形的判定与性质、三角形中位线定理、等腰三角形的性质等知识；本题综合性强，难度较大，通过作辅助线证明三角形相似是解决问题的关键．