
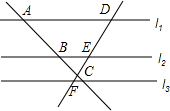
 如图,l1∥l2∥l3,两条直线与这三条平行线分别交于点A、B、C和D、E、F,已知$\frac{AB}{BC}$=$\frac{2}{3}$,则$\frac{DE}{DF}$=$\frac{2}{5}$.
如图,l1∥l2∥l3,两条直线与这三条平行线分别交于点A、B、C和D、E、F,已知$\frac{AB}{BC}$=$\frac{2}{3}$,则$\frac{DE}{DF}$=$\frac{2}{5}$.  天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
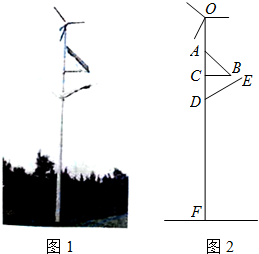 如图1,某利用风能、太阳能发电的风光互补环保路灯的灯杆顶端装有风力发电机,中间装有太阳能板,下端装有路灯.该系统工作过程中某一时刻的截面图如图2,已知太阳能板的支架BC垂直于灯杆OF,路灯顶端E距离地面6米,DE=1.8米,∠CDE=60°.且根据我市的地理位置设定太阳能板AB的倾斜角为43°,AB=1.5米,CD=1米.为保证长为1米的风力发电机叶片无障碍安全旋转,叶片与太阳能板顶端A的最近距离不少于0.5米,求灯杆OF至少要多高(利用科学计算器可求得sin43°≈0.6820,cos43°≈0.7314,tan43°≈0.9325,结果保留两位小数)?
如图1,某利用风能、太阳能发电的风光互补环保路灯的灯杆顶端装有风力发电机,中间装有太阳能板,下端装有路灯.该系统工作过程中某一时刻的截面图如图2,已知太阳能板的支架BC垂直于灯杆OF,路灯顶端E距离地面6米,DE=1.8米,∠CDE=60°.且根据我市的地理位置设定太阳能板AB的倾斜角为43°,AB=1.5米,CD=1米.为保证长为1米的风力发电机叶片无障碍安全旋转,叶片与太阳能板顶端A的最近距离不少于0.5米,求灯杆OF至少要多高(利用科学计算器可求得sin43°≈0.6820,cos43°≈0.7314,tan43°≈0.9325,结果保留两位小数)?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
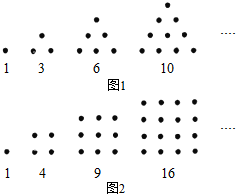 古希腊毕达哥拉斯学派的数学家常用小石子在沙滩上摆成各种形状来研究各种多边形数,比如:他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似的,称图2中的1,4,9,16,…,这样的数位正方形数(四边形数).
古希腊毕达哥拉斯学派的数学家常用小石子在沙滩上摆成各种形状来研究各种多边形数,比如:他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似的,称图2中的1,4,9,16,…,这样的数位正方形数(四边形数).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com