
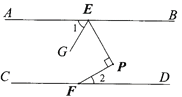
【题目】如图,已知AB∥CD,点E、F分别在直线AB、CD上,∠EPF=90°,∠BEP=∠GEP,则∠1与∠2的数量关系为( )
A. ∠1=∠2B. ∠1=2∠2C. ∠1=3∠2D. ∠1=4∠2
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,将三角形ABC向右平移5个单位长度,再向上平移3个单位长度请回答下列问题:
(1)平移后的三个顶点坐标分别为:A1 ,B1 ,C1 ;
(2)画出平移后三角形A1B1C1;
(3)求三角形ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,平面直角坐标系中,A1(1,1)、A2(﹣1,1)、A3(﹣1,﹣1)、A4(2,﹣1)、A5(2,2)、A6(﹣2,2)、A7(﹣2,﹣2)、A8(3,﹣2)、A9(3,3)、……、按此规律A2020的坐标为( )
A.(506,﹣505)B.(505,﹣504)C.(﹣504,﹣504)D.(﹣505,﹣505)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电子科技公司开发一种新产品,公司对经营的盈亏情况每月最后一天结算1次.在1~12月份中,公司前x个月累计获得的总利润y(万元)与销售时间x(月)之间满足二次函数关系式y=a(x﹣h)2+k,二次函数y=a(x﹣h)2+k的一部分图象如图所示,点A为抛物线的顶点,且点A、B、C的横坐标分别为4、10、12,点A、B的纵坐标分别为﹣16、20.
(1)试确定函数关系式y=a(x﹣h)2+k;
(2)分别求出前9个月公司累计获得的利润以及10月份一个月内所获得的利润;
(3)在前12个月中,哪个月该公司一个月内所获得的利润最多?最多利润是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】5只不透明的袋子中各装有10个球,每个球除颜色外都相同.
(1)将球搅匀,分别从每只袋子中摸一个球,摸到白球的概率一样大吗?为什么?
(2)将袋子的序号按摸到白球的概率从小到大的顺序排列.





(1) (2) (3) (4) (5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图EF∥CD,∠1+∠2=180°.
(1)试说明GD∥CA;
(2)若CD平分∠ACB,DG平分∠CDB,且∠A=40°,求∠ACB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,4),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E.那么点D的坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,![]() ,点
,点![]() 在射线
在射线![]() 上,
上,![]() .
.

(1)如图 1,若![]() ,求
,求![]() 的度数;
的度数;
(2)把“![]() °”改为“
°”改为“![]() ”,射线
”,射线![]() 沿射线
沿射线![]() 平移,得到
平移,得到![]() ,其它条件不变(如 图 2 所示),探究
,其它条件不变(如 图 2 所示),探究![]() 的数量关系;
的数量关系;
(3)在(2)的条件下,作![]() ,垂足为
,垂足为![]() ,与
,与![]() 的角平分线
的角平分线![]() 交于点
交于点![]() ,若
,若![]() , 用含 α 的式子表示
, 用含 α 的式子表示![]() (直接写出答案).
(直接写出答案).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com