
【题目】如图 ,在平面直角坐标系中 ,已知二次函数y=ax2+bx+c (a≠0)
的图象经过 A(-1,0),B(3,0),C(6,4)三点.
(1)求此二次函数解析式和顶点 D 的坐标;
(2)①E为抛物线对称轴上一点,过点E作FG//x 轴,分别交抛物线于F、G两点 ,若![]() ,求点E的坐标;
,求点E的坐标;
② 若抛物线对称轴上点 H 到直线 BC 的距离等于点 H 到 x 轴的距离,则求出点 H
的坐标;
(3)在(2)的条件下,以点I(1,![]() )为圆心,IH 的长为半径作⊙I,J 为⊙I上的动点,求是否存在一个定值
)为圆心,IH 的长为半径作⊙I,J 为⊙I上的动点,求是否存在一个定值![]() ,使得 CJ+
,使得 CJ+![]() EJ 的最小值是
EJ 的最小值是![]() 若不存在,请说明理由.若存在,请求出
若不存在,请说明理由.若存在,请求出![]() 的值;
的值;
【答案】(1)y=![]() (x+1)(x-3),对称轴为x=1,顶点坐标D(1,
(x+1)(x-3),对称轴为x=1,顶点坐标D(1,![]() )(2)
)(2)![]() 、
、![]() .(3)存在定值
.(3)存在定值![]() ,使得
,使得![]()
【解析】分析:![]() 用待定系数法求出二次函数解析式,再求出顶点坐标即可.
用待定系数法求出二次函数解析式,再求出顶点坐标即可.
![]() 分两种情况进行讨论即可.
分两种情况进行讨论即可.
![]() 假设存在,在对称轴上取点K(1,3),则
假设存在,在对称轴上取点K(1,3),则![]() ,
,![]() ,
,![]() 故
故 ![]() ,证明△IJE∽△IKJ,得到
,证明△IJE∽△IKJ,得到![]() ,即
,即![]() ,
,
从而![]() ,当且仅当K、J、C三点共线时,取得最小值.
,当且仅当K、J、C三点共线时,取得最小值.
详解:(1)设抛物线解析式为![]() ,则有
,则有
![]() ,解得
,解得![]() ,
,
故抛物线解析式为![]() ,对称轴为
,对称轴为![]() ,顶点坐标D(1,
,顶点坐标D(1,![]() ).
).
(2)①设E(1,t),则有
![]() ,
,
![]() 即
即![]()
故![]()
![]()
![]() ,
,
即![]() ,由
,由![]() ,解得
,解得![]() ,
,
∴![]() ,解得
,解得![]() ,故E(1,
,故E(1,![]() ).
).
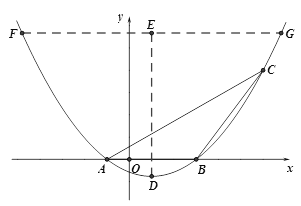
②如图,作∠ABC的平分线与对称轴x=1的交点即为符合题意的H点,记为H1;
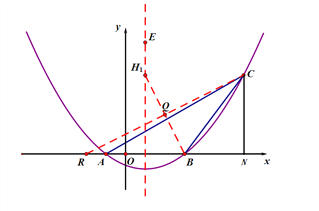
在x轴上取点R(-2,0),连结RC交∠ABC的平分线BH1于Q,则有RB=5;
过点C作CN⊥x轴交x轴于点N,
在Rt△BCN中,∵BN=3,CN=4,∴BC=5,∴BC=RB,
在△BCR中,∵BC=RB,BQ平分∠ABC,
∴Q为RC中点
∵R(-2,0),C(6,4) ∴Q(2,2),
∵B(3,0),∴过点B、Q两点的
一次函数解析式为![]()
当x=1时,y=4. 故H1(1,4)
如图,过点B作![]() 交对称轴于点H2,则点H2符合题意,记对称轴于x轴交于点T.
交对称轴于点H2,则点H2符合题意,记对称轴于x轴交于点T.
∵![]() 即
即![]()
∵![]() ,
,
∵∠BTH2=∠H1TB![]() ,∴Rt△BTH2∽Rt△H1TB,
,∴Rt△BTH2∽Rt△H1TB,
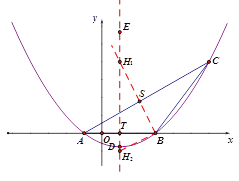
∴![]() 即
即![]()
解得![]() 即H2(1,-1)
即H2(1,-1)
综上,![]() 、
、![]() .
.
(3)存在定值![]() ,使得
,使得![]() . 理由如下:
. 理由如下:
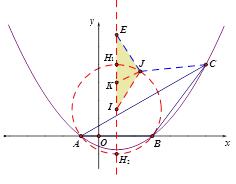
如图,在对称轴上取点K(1,3),则
![]() ,
,![]() ,
,![]()
故 ![]() ,∵∠JIE=∠KIJ,
,∵∠JIE=∠KIJ,
∴△IJE∽△IKJ,
∴![]() ,即
,即![]() ,
,
从而![]() ,当且仅当K、J、C三点共线时,
,当且仅当K、J、C三点共线时,![]() ,即
,即![]() ,
,
故存在定值![]() ,使得
,使得![]() .
.


科目:初中数学 来源: 题型:
【题目】一个寻宝游戏的寻宝通道如图①所示,通道由在同一平面内的AB,BC,CA,OA, OB,OC组成。为记录寻宝者的行进路线,在BC的中点M处放置了一台定位仪器,设寻宝者行进的时间为x,寻宝者与定位仪器之间的距离为y,若寻宝者匀速行进,且表示y与x的函数关系的图像大致如图②所示,则寻宝者的行进路线可能为:

A. A→O→B B. B→A→C C. B→O→C D. C→B→O
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大?题中“里”是我国市制长度单位,1里=0.5千米,则该沙田的面积为________________平方千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知P为正方形ABCD外的一点,PA=1,PB=2,将△ABP绕点B顺时针旋转90°,使点P旋转至点P′,且AP′=3,则∠BP′C的度数为 ( )
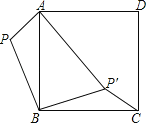
A.105° B.112.5° C.120° D.135°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文化用品商店用1 000元购进一批“晨光”套尺,很快销售一空;商店又用1 500元购进第二批该款套尺,购进时单价是第一批的![]() 倍,所购数量比第一批多100套.
倍,所购数量比第一批多100套.
(1)求第一批套尺购进时单价是多少?
(2)若商店以每套4元的价格将这两批套尺全部售出,可以盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
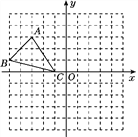
【题目】如图,已知网格上最小的正方形的边长为1.
(1)分别写出A,B,C三点的坐标;
(2)作△ABC关于y轴的对称图形△A′B′C′(不写作法),想一想:关于y轴对称的两个点之间有什么关系?
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
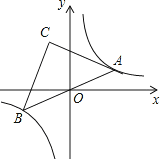
【题目】如图,点A是双曲线y=![]() 在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为 .
在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠APB=30°,圆心在PB上的⊙O的半径为1cm,OP=3cm,若⊙O沿BP方向平移,当⊙O与PA相切时,圆心O平移的距离为_____cm.
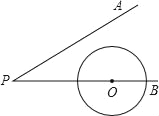
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com