
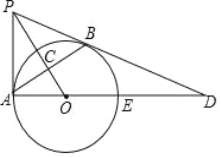
【题目】如图,PB与⊙O相切于点B,过点B作OP的垂线BA,垂足为C,交⊙O于点A,连结PA,AO,AO的延长线交⊙O于点E,与PB的延长线交于点D.
(1)求证:PA是⊙O的切线;
(2)若tan∠BAD=![]() ,且OC=4,求BD的长.
,且OC=4,求BD的长.
【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)连接OB,由SSS证明△PAO≌△PBO,得出∠PAO=∠PBO=90°即可;
(2)连接BE,证明△PAC∽△AOC,证出OC是△ABE的中位线,由三角形中位线定理得出BE=2OC,由△DBE∽△DPO可求出.
试题解析:(1)连结OB,则OA=OB.如图1,
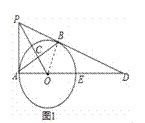
∵OP⊥AB,
∴AC=BC,∴OP是AB的垂直平分线,∴PA=PB.
在△PAO和△PBO中,
∵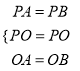 ,
,
∴△PAO≌△PBO(SSS),
∴∠PBO=∠PAO.∵PB为⊙O的切线,B为切点,∴∠PBO=90°,
∴∠PAO=90°,即PA⊥OA,∴PA是⊙O的切线;
(2)连结BE.如图2,
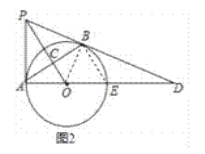
∵在Rt△AOC中,tan∠BAD=tan∠CAO=![]() ,且OC=4,
,且OC=4,
∴AC=6,则BC=6.在Rt△APO中,∵AC⊥OP,
∴△PAC∽△AOC,∴AC2=OCPC,解得PC=9,
∴OP=PC+OC=13.在Rt△PBC中,由勾股定理,得PB=![]() ,
,
∵AC=BC,OA=OE,即OC为△ABE的中位线.
∴OC=![]() BE,OC∥BE,∴BE=2OC=8.
BE,OC∥BE,∴BE=2OC=8.
∵BE∥OP,∴△DBE∽△DPO,
∴![]() ,即
,即![]() ,解得BD=
,解得BD=![]() .
.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
【题目】某学校开展“青少年科技创新比赛”活动,“喜洋洋”代表队设计了一个遥控车沿直线轨道AC做匀速直线运动的模型.甲、乙两车同时分别从A,B两处出发,沿轨道到达C处,B在AC上,甲的速度是乙的速度的1.5倍,设t(分)后甲、乙两遥控车与B处的距离分别为d1,d2,则d1,d2与t的函数关系如图,试根据图象解决下列问题:
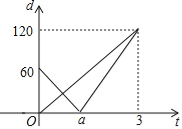
(1)填空:乙的速度v2= 米/分;
(2)写出d1与t的函数关系式:
(3)若甲、乙两遥控车的距离超过10米时信号不会产生相互干扰,试探求什么时间两遥控车的信号不会产生相互干扰?
查看答案和解析>>
科目:初中数学 来源: 题型:
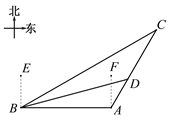
【题目】如图,某天我国一艘海监船巡航到A港口正西方的B处时,发现在B的北偏东60°方向,相距150海里处的C点有一可疑船只正沿CA方向行驶,C点在A港口的北偏东30°方向上,海监船向A港口发出指令,执法船立即从A港口沿AC方向驶出,在D处成功拦截可疑船只,此时D点与B点的距离为75![]() 海里.
海里.
(1)求B点到直线CA的距离;
(2)执法船从A到D航行了多少海里?(![]() ≈1.414,
≈1.414,![]() ≈1.732,结果精确到0.1海里)
≈1.732,结果精确到0.1海里)
查看答案和解析>>
科目:初中数学 来源: 题型:
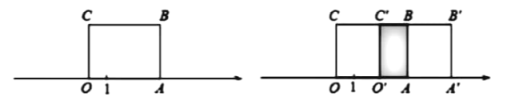
【题目】如图1,长方形![]() 的边
的边![]() 在数轴上,
在数轴上,![]() 为原点,长方形
为原点,长方形![]() 的面积为12,
的面积为12,![]() 边的长为3.
边的长为3.
(1)数轴上点![]() 表示的数为________.
表示的数为________.
(2)将长方形![]() 沿数轴水平移动,移动后的长方形记为
沿数轴水平移动,移动后的长方形记为![]() ,设长方形
,设长方形![]() 移动的距离为
移动的距离为![]() ,移动后的长方形
,移动后的长方形![]() 与原长方形
与原长方形![]() 重叠部分的面积记为
重叠部分的面积记为![]() .
.
①当![]() 等于原长方形
等于原长方形![]() 面积的
面积的![]() 时,则点
时,则点![]() 的移动距离
的移动距离![]() _______,此时数轴上点
_______,此时数轴上点![]() 表示的数为_______.
表示的数为_______.
②![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上,且
上,且![]() 当点
当点![]() ,
,![]() 所表示的数互为相反数时,则
所表示的数互为相反数时,则![]() 的值为_______.
的值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】怡然美食店的A、B两种菜品,每份成本均为14元,售价分别为20元、18元,这两种菜品每天的营业额共为1120元,总利润为280元.
(1)该店每天卖出这两种菜品共多少份?
(2)该店为了增加利润,准备降低A种菜品的售价,同时提高B种菜品的售价,售卖时发现,A种菜品售价每降0.5元可多卖1份;B种菜品售价每提高0.5元就少卖1份,如果这两种菜品每天销售总份数不变,那么这两种菜品一天的总利润最多是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
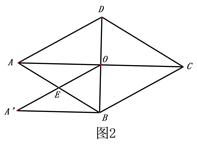
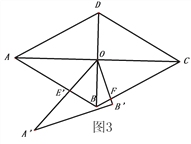
【题目】如图1,菱形ABCD,AB=4,∠ADC=120o,连接对角线AC、BD交于点O,
(1)如图2,将△AOD沿DB平移,使点D与点O重合,求平移后的△A′BO与菱形ABCD重合部分的面积.
(2)如图3,将△A′BO绕点O逆时针旋转交AB于点E′,交BC于点F,
①求证:BE′+BF=2,
②求出四边形OE′BF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B两点在反比例函数y=![]() 的图象上,C,D两点在反比例函数y=
的图象上,C,D两点在反比例函数y=![]() 的图象上,AC⊥x轴于点E,BD⊥x轴于点F,AC=2,BD=3,EF=
的图象上,AC⊥x轴于点E,BD⊥x轴于点F,AC=2,BD=3,EF=![]() ,则k2-k1的值为( )
,则k2-k1的值为( )

A. 4 B. ![]() C.
C. ![]() D. 6
D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于任意有理数a,b,定义运算:a⊙b=a(a+b)﹣1,等式右边是通常的加法、减法、乘法运算,例如,2⊙5=2×(2+5)﹣1=13;(﹣3)⊙(﹣5)=﹣3×(﹣3﹣5)﹣1=23.
(1)求(﹣2)⊙3![]() 的值;
的值;
(2)对于任意有理数m,n,请你重新定义一种运算“⊕”,使得5⊕3=20,写出你定义的运算:m⊕n= (用含m,n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线y=x2+bx+c过A,B,C三点,点A的坐标是(3,0),点C的坐标是(0,-3),动点P在抛物线上.
(1)b =_________,c =_________,点B的坐标为_____________;(直接填写结果)
(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com