【题目】如图，正方形
中，
，
是对角线
上的一个动点，若
的最小值是10，则
长为___________．
【答案】
【解析】
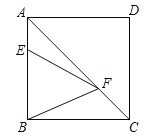
如图，连接DF，DE，DE交AC于F′，连接BF′．由BF+EF=EF+DF≤DE，推出当点F与点F′重合时，BF+EF的值最小，最小值为线段DE的长，由题意AE=
AB，设AE=a，则AB=3a，在Rt△AEB中，根据AE2+AD2=DE2，构建方程即可解决问题．
如图，连接DF，DE，DE交AC于F′，连接BF′
∵四边形ABCD是正方形
∴BF=DF
∵BF+EF=EF+DFDE
∴当点F与点F′重合时，BF+EF的值最小，最小值为线段DE的长
由题意AE=AB，设AE=a，则AB=3a
在Rt△AEB中，∵AE2+AD2=DE2
∴a2+9a2=100
∴a=
∴AB=3a=
故答案为：
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
【题目】如图，以OA为边的△OAB面积为2，其中点B的横、纵坐标均不超过4，且都不小于0，在下列叙述中，正确的是：_____．（请写出所有正确的选项）
①若点B的横坐标是4，则满足条件的点B有且只有1个；
②若点B是整点（即横、纵坐标都是整数），则满足条件的点B有4个；
③在坐标系内，对于任意满足题意的点B，一定存在一点C，使得△CAB、△COA、△COB面积相等；
④在坐标系内，存在一个定点D，使得对于任意满足条件的点B，△DBA、△DBO面积相等．
查看答案和解析>>
科目：初中数学 来源： 题型：
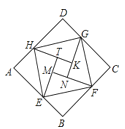
【题目】如图是由“赵爽弦图”变化得到的，它由八个全等的直角三角形拼接而成，记图中正方形ABCD，正方形EFGH，正方形MNKT的面积分别为
,若
，则
的值是_______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】以点A为顶点作两个等腰直角三角形（△ABC，△ADE），如图1所示放置，使得一直角边重合，连接BD，CE．
（1）说明BD=CE；
（2）延长BD，交CE于点F，求∠BFC的度数；
（3）若如图2放置，上面的结论还成立吗？请简单说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，O是矩形ABCD的对角线的交点，DE∥AC，CE∥BD．
（1）求证：OE⊥DC．
（2）若∠AOD＝120°，DE＝2，求矩形ABCD的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在长方形ABCD中，O为平面直角坐标系的原点，点的坐标分别为A(a，2)、B(a，-1)，D(b，2)．且a、b满足
．点P从A点出发，以每秒1个单位长度的速度A-B-C-D-A的线路移动，运动时间为t，当点P回到A点时运动停止
（1）点C的坐标为_______________
（2）当点P移动在线段BC上时，求三角形ACP的面积（用含t的代数式表示）
（3）在移动过程中，当三角形ACP的面积是5时，直接写出点P移动的时间为几秒
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】完成下面的证明过程：
如图所示，直线AD与AB，CD分别相交于点A，D，与EC，BF分别相交于点H，G，已知∠1＝∠2，∠B＝∠C．
求证：∠A＝∠D．
证明：∵∠1＝∠2，（已知）∠2＝∠AGB（ ）
∴∠1＝ （ ）
∴EC∥BF（ ）
∴∠B＝∠AEC（ ）
又∵∠B＝∠C（已知）
∴∠AEC＝ （ ）
∴ （ ）
∴∠A＝∠D（ ）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，∠ABD、∠ACD的角平分线交于点P，若∠A = 50°,∠D =10°，则∠P的度数为( )
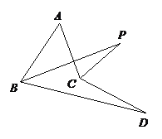
A.15°B.20°C.25°D.30°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某工厂甲、乙两个部门各有员工400人，为了解这两个部门员工的生产技能情况，进行了抽样调查，过程如下，请补充完整：收集数据：从甲、乙两个部门各随机抽取20名员工，进行了生产技能测试，测试成绩（百分）如下：
甲 | 78 | 86 | 74 | 81 | 75 | 76 | 87 | 70 | 75 | 90 |
75 | 79 | 81 | 70 | 74 | 80 | 86 | 69 | 83 | 77 | |
乙 | 93 | 73 | 88 | 81 | 72 | 81 | 94 | 83 | 77 | 83 |
80 | 81 | 70 | 81 | 73 | 78 | 82 | 80 | 70 | 40 |
（1）整理、描述数据：按如分数段整理、描述这两组样本数据（请补全表格）：
|
|
|
|
|
| |
甲 | 0 | 0 | 1 | 11 | 7 | 1 |
乙 | __________ | 0 | 0 | __________ | __________ | __________ |
（说明：成绩80分及以上为生产技能优秀，70-79分为生产技能良好，60-69分为生产技能合格，60分以下为生产技能不合格）
分析数据：两组样本数据的平均数、中位数、众数如表所示（请补全表格）：
部门 | 平均数 | 中位数 | 众数 |
甲 | 78.3 | __________ | 75 |
乙 | 78 | 80.5 | __________ |
得出结论：
（2）估计乙部门生产技能优秀的员工人数为__________；
（3）你认为__________部门员工的生产技能水平较高，说明理由（至少从两个不同的角度说明推断的合理性）．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
