
 如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=6cm,∠ABD=30°,则⊙O的面积为( )
如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=6cm,∠ABD=30°,则⊙O的面积为( )| A. | 25πcm2 | B. | 49πcm2 | C. | 32πcm2 | D. | 36πcm2 |
分析 首先连接OD,OC,由∠ABD=30°,根据圆周角定理,可求得∠AOD=60°,又由BC=CD=6cm,可得∠AOD=∠COD=∠BOC=60°,即可求得AD的长,又由直径所对的圆周角是直角,可得∠ADB=90°,继而求得AB的长,则可求得答案.
解答 解:连接OD,OC,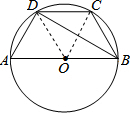
∵∠ABD=30°,
∴∠AOD=2∠ABD=60°,
∴∠BOD=120°,
∵BC=CD=6cm,
∴∠BOC=∠COD=60°,
∴∠AOD=∠BOC=∠COD,
∴AD=BC=6cm,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴AB=2AD=12cm,
∴⊙O的面积为:36πcm2.
故选D.
点评 此题考查了圆周角定理以及弧与弦的关系.注意准确作出辅助线是解此题的关键.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 人均住房面积(平方米) | 单价(万元/平方米) |
| 不超过30平方米 | 0.6 |
| 超过30平方米不超过m平方米的部分(45≤m≤60) | 0.8 |
| 超过m平方米部分 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com