练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．如图，将一个三角板与一把直尺叠放在一起，使三角板的直角顶点C在直尺的一边上，若∠1=31°18′，则∠2的度数为58°42′．

    分析 先根据直角与∠1，求得∠ACD的度数，再根据平行线的性质，求得∠2的度数．

    解答 解：∵∠ACB=90°，∠1=31°18′，
    ∴∠ACD=90°-31°18′=58°42′，
    ∵直尺的对边平行，
    ∴∠2=∠ACD=58°42′．
    故答案为：58°42′．

    点评 本题主要考查了平行线的性质，解决问题的关键是运用两直线平行，同位角相等进行求解．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    17．如图，已知AB⊥AD，BD⊥DC，且BD2=AB•BC，求证：∠ABD=∠DBC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．如图，⊙O是△ABC的外接圆，若⊙O的半径为2.5，AC=3，AC≠AB，则tanB的值为$\frac{3}{4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．若ab≠0，则$\frac{a}{|a|}$+$\frac{|b|}{b}$不等于-2，0，1，2这四个数中的（　　）
    A．-2B．0C．1D．2

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．已知关于x的一元二次方程（b-c）x2+（c-a）x+（a-b）=0有两个相等的实数根，则实数a，b，c之间的关系是2b=a+c．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

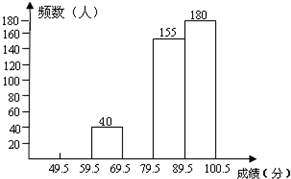    12．某区初中有10000名学生参加安全应急预案知识竞赛活动，为了了解本次知识竞赛的成绩分布情况，从中抽取了500名学生的得分（得分取正整数，满分100分）进行统计：
    频率分布表
    分  组频  数频  率
    49.5～59.525
    59.5～69.5400.08
    69.5～79.50.20
    79.5～89.5155
    89.5～100.51800.36
    合  计5001
    请你根据不完整的频率分布表．解答下列问题：
    （1）补全频率分布表；   
    （2）补全频数分布直方图；
    （3）若将得分转化为等级，规定得分低于59.5分评为“D”，59.5～69.5分评为“C”，69.5～89.5分评为“B”，89.5～100.5分评为“A”，估计这次10000名学生中约有多少人评为“D”？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．一个正数的两个平方根是2a-1与-a+4，则a=-3，这个正数是25．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．如图，在锐角△ABC中，D、E分别是AB、AC上的点，△ADC≌△ADC′，△AEB≌△AEB′，且C′D∥EB′∥BC，BE、CD相交于点F．若∠BAC=35°，则∠BFC=110°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．如图1，抛物线y=ax2+bx-3与y轴于点，与x轴交于A、B两点，OB=3OA，∠ABC=45°
    （1）求此抛物线的解析式；
    （2）如图2，平移此抛物线使其顶点为坐标原点，点M为y轴上一动点，MN与抛物线只有唯一公共点N点，点G在x轴上，∠GNM=∠OMN，求证：直线NG必过一定点，并求此定点的坐标．

    查看答案和解析>>

    同步练习册答案