练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
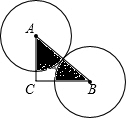
    4．如图，Rt△ABC中，∠C=90°，AC=4，BC=4$\sqrt{3}$，两等圆⊙A，⊙B外切，那么图中两个扇形（即阴影部分）的面积之和为（　　）
    A．2πB．4πC．6πD．8π

    分析 先依据勾股定理求得AB的长，从而可求得两圆的半径为4，然后由∠A+∠B=90°可知阴影部分的面积等于一个圆的面积的$\frac{1}{4}$．

    解答 解：在△ABC中，依据勾股定理可知AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=8．
    ∵两等圆⊙A，⊙B外切，
    ∴两圆的半径均为4．
    ∵∠A+∠B=90°，
    ∴阴影部分的面积=$\frac{90π×{4}^{2}}{360}$=4π．
    故选：B．

    点评 本题主要考查的是相切两圆的性质、勾股定理的应用、扇形面积的计算，求得两个扇形的半径和圆心角之和是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    14．太阳的表面温度大约有6000℃，而太阳中心的温度达到了1920万℃，其中“1920万”用科学记数法可将表示为（　　）
    A．1.92×103B．1.92×107C．19.2×102D．0.192×108

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

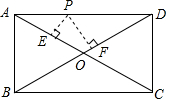    15．如图，P是矩形ABCD的边AD上一个动点，PE⊥AC于E，PF⊥BD于F，当P从A向D运动（P与A，D不重合），则PE+PF的值（　　）
    A．增大B．减小C．不变D．先增大再减小

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．不等式组$\left\{\begin{array}{l}{2x-1≤1}\\{x+1＞-2}\end{array}\right.$的解集在数轴上表示为（　　）
    A．B．
    C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．在同一坐标系中一次函数y=ax-b和二次函数y=ax2+bx的图象可能为（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．据河南省发改委发布消息，2016年全省固定资产投资继续保持持续稳定增长，全年完成39753亿元，总量居全国第3位．将数据39753亿用科学记数法表示为（　　）
    A．3.9753×109B．0.39753×1010C．39.753×1011D．3.9753×1012

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

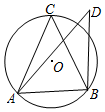    16．如图，锐角△ABC内接于⊙O，点D在⊙O外（与点C在AB同侧），∠ABD=90°，下列结论：①sinC＞sinD；②cosC＞cosD；③tanC＞tanD，正确的结论为（　　）
    A．①②B．②③C．①②③D．①③

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．下列各式计算正确的是（　　）
    A．a2+a2=a4B．（-2x）3=-8x3C．a3•a4=a12D．（x-3）2=x2-9

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

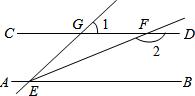    14．如图，已知直线AB∥CD，∠GEB的平分线EF交CD于点F，∠1=60°，则∠2等于（　　）
    A．130°B．140°C．150°D．160°

    查看答案和解析>>

    同步练习册答案