
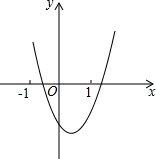
 二次函数y=ax2+bx+c的图象如图所示,请写出一次函数y=bx+b2-4ac与反比例函数y=$\frac{a+b+c}{x}$的图象分别经过哪几个象限?并说明理由.
二次函数y=ax2+bx+c的图象如图所示,请写出一次函数y=bx+b2-4ac与反比例函数y=$\frac{a+b+c}{x}$的图象分别经过哪几个象限?并说明理由. 分析 把x=1代入二次函数解析式,结合图象得到a+b+c<0,由此得到反比例函数的系数k<0,由反比例函数图象与系数的关系进行解答.
解答  解:如图所示,抛物线开口向上,则a>0.
解:如图所示,抛物线开口向上,则a>0.
又∵对称轴在y轴的由右侧,
∴a、b异号,
∴b<0,
∴一次函数y=bx+b2-4ac经过第一、二、四象限.
如图所示,当x=1时,y<0,即a+b+c<0,
又抛物线与x轴有2个交点,则+b2-4ac>0.
∴反比例函数y=$\frac{a+b+c}{x}$的系数小于0,
∴反比例函数y=$\frac{a+b+c}{x}$的图象经过第二、四象限.
点评 本题考查了反比例函数的性质,二次函数的性质以及一次函数图象与系数的关系.熟记函数图象性质即可解题.


科目:初中数学 来源: 题型:选择题
 如图,⊙O中,弦AB=2,点C在⊙O上,∠ACB=45°,则⊙O的半径等于( )
如图,⊙O中,弦AB=2,点C在⊙O上,∠ACB=45°,则⊙O的半径等于( )| A. | $\sqrt{2}$ | B. | 1 | C. | 2$\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 阅读:|5-2|表示5与2差的绝对值,也可理解为5与2两位数在数轴上所对应的两点之间的距离;|5+2|可以看做|5-(-2)|,表示5与-2的差的绝对值,也可理解为5与-2两位数在数轴上所对应的两点之间的距离,探索:
阅读:|5-2|表示5与2差的绝对值,也可理解为5与2两位数在数轴上所对应的两点之间的距离;|5+2|可以看做|5-(-2)|,表示5与-2的差的绝对值,也可理解为5与-2两位数在数轴上所对应的两点之间的距离,探索:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图△ABC中,tan∠C=$\frac{1}{2}$,DE⊥AC,若CE=5,DE=1,且△BEC的面积是△ADE面积的10倍,则BE的长度是$\sqrt{5}$.
如图△ABC中,tan∠C=$\frac{1}{2}$,DE⊥AC,若CE=5,DE=1,且△BEC的面积是△ADE面积的10倍,则BE的长度是$\sqrt{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com