
【题目】如图,线段CD在线段AB上,且CD=2,若线段AB的长度是一个正整数,则图中以A,B,C,D这四点中任意两点为端点的所有线段长度之和可能是( ) ![]()
A.28
B.29
C.30
D.31
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图数轴的A,B,C三点所表示的数分别为a、b、c.若|a﹣b|=3,|b﹣c|=5,且原点O与A,B的距离分别为4、1,则关于O的位置,下列叙述何者正确?( ) ![]()
A.在A的左边
B.介于A,B之间
C.介于B,C之间
D.在C的右边
查看答案和解析>>
科目:初中数学 来源: 题型:
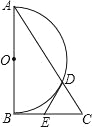
【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径作半圆⊙O交AC与点D,点E为BC的中点,连接DE.
(1)求证:DE是半圆⊙O的切线.
(2)若∠BAC=30°,DE=2,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
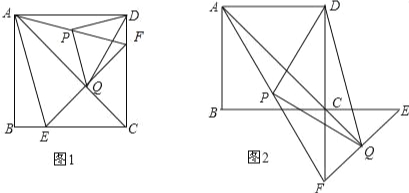
【题目】如图1,在正方形ABCD中,点E、F分别在边BC、CD上,且BE=DF,点P是AF的中点,点Q是直线AC与EF的交点,连接PQ、PD.
(1)求证:AC垂直平分EF;
(2)试判断△PDQ的形状,并加以证明;
(3)如图2,若将△CEF绕着点C旋转180°,其余条件不变,则(2)中的结论还成立吗?若成立,请加以证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校组织植树活动,已知在甲处植树的有14人,在乙处植树的有6人,现调70人去支援.
(1)若要使在甲处植树的人数与在乙处植树的人数相等,应调往甲处人.
(2)若要使在甲处植树的人数是在乙处植树人数的2倍,问应调往甲、乙两处各多少人?
(3)通过适当的调配支援人数,使在甲处植树的人数恰好是在乙处植树人数的n倍(n是大于1的正整数,不包括1.)则符合条件的n的值共有个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,最适宜采用抽样调查方式的是()
A.对神州十一号载人航天飞船各零部件的检查B.对重庆市初中学生每天的锻炼情况的调查
C.对乘坐飞机的旅客是否携带了违禁物品的调查D.对某校九年级一班同学数学成绩的调查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)请在横线上填写合适的内容,完成下面的证明:
如图1,AB∥CD,求证:∠B+∠D=∠BED.
证明:过点E引一条直线EF∥AB
∴∠B=∠BEF,( )
∵AB∥CD,EF∥AB
∴EF∥CD( )
∴∠D=( )
∴∠B+∠D=∠BEF+∠FED
即∠B+∠D=∠BED.
(2)如图2,AB∥CD,请写出∠B+∠BED+∠D=360°的推理过程.
(3)如图3,AB∥CD,请直接写出结果∠B+∠BEF+∠EFD+∠D= 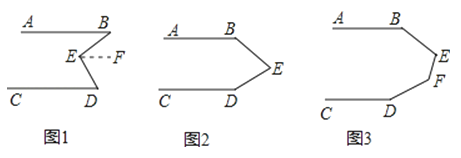
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com