
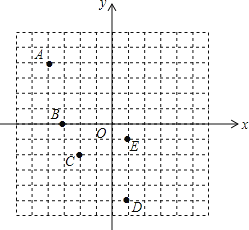
【题目】在平面直角坐标系中,每个小方格的边长为一个单位长度.
(1)点![]() 的坐标为 .点
的坐标为 .点![]() 的坐标为 .
的坐标为 .
(2)点![]() 关于
关于![]() 轴对称点的坐标为 ;
轴对称点的坐标为 ;
(3)以![]() 、
、![]() 、
、![]() 为顶点的三角形的面积为 ;
为顶点的三角形的面积为 ;
(4)点![]() 在
在![]() 轴上,且
轴上,且![]() 的面积等于
的面积等于![]() 的面积,点
的面积,点![]() 的坐标为 .
的坐标为 .
【答案】(1)![]() ;
;![]() ;(2)
;(2) ![]() ;(3)6 ;(4)
;(3)6 ;(4)![]() ;
;![]()
【解析】
(1)根据图形可得出点的坐标即可;
(2)根据关于x轴对称点的坐标特点:横坐标相等,纵坐标互为相反数,即可得出结果;
(3)以DE为底边,根据三角形的面积公式解答即可;
(4)以BP为底边,根据三角形的面积公式和x轴上坐标的特点解答即可.
解:(1)据图可得点A的坐标为(-4,4),点B的坐标为(-3,0),
故答案为:(-4,4)(-3,0);
(2)点C的坐标为(-2,-2,),可得点C关于x轴对称点的坐标为(-2,2);
故答案为:(-2,2);
(3)如图,作出△CDE,由图可知DE∥y轴,过点C作CH⊥DE于H,则根据点的坐标可知,DE=4,CH=3.
∴S△CDE=![]() ×4×3=6,
×4×3=6,
故答案为:6;

(4)因为△ABP的面积等于△CDE的面积=6,设点P的坐标为(x,0),则
6=![]() ×|x-(-3)|×4,解得x=0,或x=-6.
×|x-(-3)|×4,解得x=0,或x=-6.
∴点P坐标为:(-6,0)(0,0),
故答案为:(-6,0)(0,0).


科目:初中数学 来源: 题型:
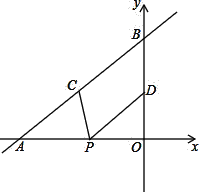
【题目】如图,直线y=x+4与x轴、y轴分别交于点A和点B,点D为线段OB的中点,点C、P分别为线段AB、OA上的动点,当PC+PD值最小时点P的坐标为_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点A(2,0),点B (0,1),过点A的直线l垂直于线段AB,点P是直线l上一动点,过点P作PC⊥x轴,垂足为C,把△ACP沿AP翻折![]() ,使点C落在点D处,若以A,D,P为顶点的三角形与△ABP相似,则所有满足此条件的点P的坐标为___________________________.
,使点C落在点D处,若以A,D,P为顶点的三角形与△ABP相似,则所有满足此条件的点P的坐标为___________________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
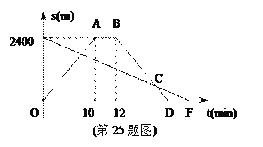
【题目】小明从家骑自行车出发,沿一条直路到相距2400m的邮局办事,小明出发的同时,他的爸爸以96m/min速度从邮局同一条道路步行回家,小明在邮局停留2min后沿原路以原速返回,设他们出发后经过t min时,小明与家之间的距离为s1m,小明爸爸与家之间的距离为s2 m,图中折线OABD、线段EF分别表示s1、s2与t之间的函数关系的图象。
(1)求s2与t之间的函数关系式;
(2)小明从家出发,经过多长时间在返回途中追上爸爸?这时他们距离家还有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”节假期间,小亮一家到某度假村度假,小亮和他妈妈坐公交车先出发,他爸爸自驾车沿着相同的道路后出发,他爸爸到达度假村后,发现忘了东西在家里,于是立即返回家里取,取到东西后又马上驾车前往度假村,如图是他们家的距离![]() (
(![]() )与小明离家的时间
)与小明离家的时间![]() 的关系图,请根据图回答下列问题:
的关系图,请根据图回答下列问题:
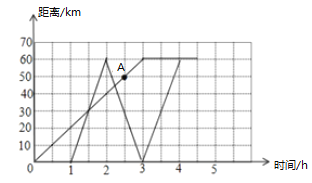
(1)小亮和妈妈坐公交车的速度为 ![]() ;爸爸自驾的速度为
;爸爸自驾的速度为 ![]() .
.
(2)小亮从家到度假村期间,他离家的距离![]() 与离家的时间
与离家的时间![]() 的关系式为 ;小亮从家到度假村的路途中,当他与他爸爸相遇时,离家的距离是
的关系式为 ;小亮从家到度假村的路途中,当他与他爸爸相遇时,离家的距离是 ![]() .
.
(3)整个运动过程中(双方全部到达会和时,视为运动结束),![]() 为多少时小亮和妈妈与爸爸相距
为多少时小亮和妈妈与爸爸相距![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,AM是△ABC的外角∠CAE的平分线.

(1)如图1,求证:AM∥BC;
(2)如图2,若D是BC中点,DN平分∠ADC交AM于点N,DQ平分∠ADB交AM的反向延长线于Q,判断△QDN的形状并说明理由.
(3)如图3,在(2)的条件下,若∠BAC=90°将∠QDN绕点D旋转一定角度,DN交边AC于F,DQ交边AB于H,当S△ABC=14时,则四边形AHDF的面积为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com