
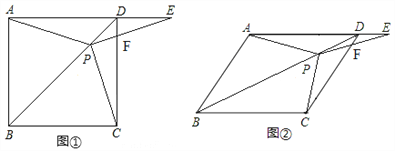
【题目】如图①,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PE=PA,PE交CD于F.
(1)求证: PC=PE;
(2)求∠CPE的度数;
(3)如图②,把正方形ABCD改为菱形ABCD,其它条件不变,若∠ABC=65°,则∠CPE=________度.
【答案】(1)证明见解析;(2)90°;(3)115°
【解析】试题分析:(1)先证出△ABP≌△CBP,得PA=PC,由于PA=PE,得PC=PE;
(2)由△ABP≌△CBP,得∠BAP=∠BCP,进而得∠DAP=∠DCP,由PA=PC,得到∠DAP=∠E,∠DCP=∠E,最后∠CPF=∠EDF=90°得到结论;
(3)借助(1)和(2)的证明方法容易证明结论.
试题解析:(1)在正方形ABCD中,AB=BC,
∠ABP=∠CBP=45°,
在△ABP和△CBP中,
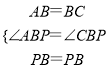 ,
,
∴△ABP≌△CBP(SAS),
∴PA=PC,
∵PA=PE,
∴PC=PE;
(2)由(1)知,△ABP≌△CBP,
∴∠BAP=∠BCP,
∵PA=PE,
∴∠PAE=∠PEA,
∴∠CPB=∠AEP,
∵∠AEP+∠PEB=180°,
∴∠PEB+∠PCB=180°,
∴∠ABC+∠EPC=180°,
∵∠ABC=90°,
∴∠EPC=90°;
(3)∠EPC=115°,
理由:在菱形ABCD中,AB=BC,∠ABP=∠CBP,
在△ABP和△CBP中,
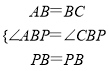 ,
,
∴△ABP≌△CBP(SAS),
∴∠BAP=∠BCP,
∵PA=PE,
∴∠DAP=∠DCP,
∴∠PAE=∠PEA,
∴∠CPB=∠AEP,
∵∠AEP+∠PEB=180°,
∴∠PEB+∠PCB=180°,
∴∠ABC+∠EPC=180°.
∴∠CPE=180°-∠ABC=180°-65°=115°


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:
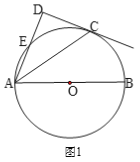
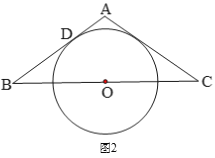
【题目】(1)如图1,点C在以AB为直径的⊙O上,AD与过点C的切线CD垂直,垂足为点D.
求证:AC平分∠DAB;
(2)如图2,△ABC为等腰三角形,AB=AC,O是BC的中点,AB与⊙O相切于点D.
求证:![]() 是⊙
是⊙![]() 的切线.
的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了“创建文明城市,建设美丽家园”,我市某社区将辖区内的一块面积为1000m2的空地进行绿化,一部分种草,剩余部分栽花,设种草部分的面积为![]() (m2),种草所需费用
(m2),种草所需费用![]() 1(元)与
1(元)与![]() (m2)的函数关系式为
(m2)的函数关系式为 ,其图象如图所示:栽花所需费用
,其图象如图所示:栽花所需费用![]() 2(元)与x(m2)的函数关系式为
2(元)与x(m2)的函数关系式为![]() 2=﹣0.01
2=﹣0.01![]() 2﹣20
2﹣20![]() +30000(0≤
+30000(0≤![]() ≤1000).
≤1000).

(1)请直接写出k1、k2和b的值;
(2)设这块1000m2空地的绿化总费用为W(元),请利用W与![]() 的函数关系式,求出绿化总费用W的最大值;
的函数关系式,求出绿化总费用W的最大值;
(3)若种草部分的面积不少于700m2,栽花部分的面积不少于100m2,请求出绿化总费用W的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,动点E以每秒1个单位长度的速度从点A开始沿边AB向点B运动,动点F以每秒2个单位长度的速度从点B开始沿边BC向点C运动,动点E比动点F先出发1秒,其中一个动点到达终点时,另一个动点也随之停止运动设点F的运动时间为t秒.
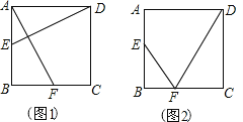
(1)如图1,连接DE,AF.若DE⊥AF,求t的值;
(2)如图2,连结EF,DF.当t为何值时,△EBF∽△DCF?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】投资1万元围一个矩形菜园(如图),其中一边靠墙,另外三边选用不同材料建造.墙长24 m,平行于墙的边的费用为200元/m,垂直于墙的边的费用为150元/m,设平行于墙的边长为x m.
(1)设垂直于墙的一边长为y m,直接写出y与x之间的函数关系式;
(2)若菜园面积为384 m2,求x的值;
(3)求菜园的最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,AB∥y轴,AB=3,反比例函数y=-![]() 的图象经过点B,与AC交于点D,且CD=2AD,则点D的横坐标是( )
的图象经过点B,与AC交于点D,且CD=2AD,则点D的横坐标是( )

A.-1B.-2C.-3D.-4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,AB=4,点C,点D在⊙O上,CD=2,直线AD,BC交于点E.
(1)如图,若点E在⊙O外,求∠AEB的度数.
(2)若DC∥AB,试求出△ABE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
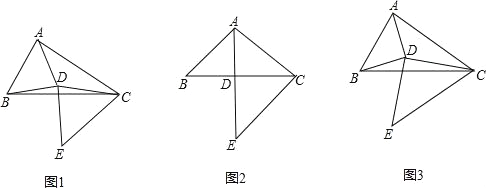
【题目】如图1,在△ABC中,BC=4,以线段AB为边作△ABD,使得AD=BD,连接DC,再以DC为边作△CDE,使得DC=DE,∠CDE=∠ADB=α.
(1)如图2,当∠ABC=45°且α=90°时,用等式表示线段AD,DE之间的数量关系;
(2)将线段CB沿着射线CE的方向平移,得到线段EF,连接BF,AF.
①若α=90°,依题意补全图3,求线段AF的长;
②请直接写出线段AF的长(用含α的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com