
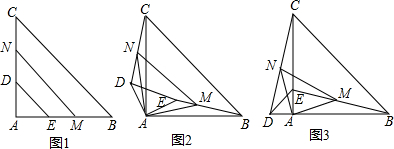
分析 (1)利用等式的性质直接得到,BE=CD,用中点和BE=CD,先判断出AM=AN即可;
(2)由全等三角形得到∠MAB=∠NAC,再由直角三角形两锐角互余,判断出BE⊥CD;
(2)由(2)的结论BE=CD,∠MAB=∠CAN,再判断出∠MAN=90°,即可.
解答 解:(1)∵AB=AC,AD=AE.
∴AC-AD=AB-AE,
∴BE=CD;
∵M、N分别是EB、CD的中点,
∴DN=$\frac{1}{2}$CD,EM=$\frac{1}{2}$BE,
∴AN=AM,
∵∠BAC=90°,
∴△AMN是等腰直角三角形;
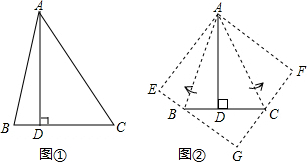
(2)如图,延长BE,CD交于点G,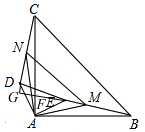
由旋转得,∠BAM=∠CAD,
∵AE=AD,AB=AC,∴△AMB≌△ADC,
∴BE=CD,∠ABM=∠ACD,
∵∠BAC=∠DAE=90°,
∴∠CAE+∠BAE=90°,
∴∠CAE+∠ACN=90°,
∵∠AFE=∠CFG,
∴∠ACN+∠CAE=90°,
∴∠CGE=90°,
∴BE⊥CD;
(3)△AMN是等腰直角三角形,
由(1)有,AM=AN,∠MAB=∠CAN,
∵∠CAM+∠MAB=∠CAM+∠CAN=∠MAN=90°,
∴△AMN是等腰直角三角形.
点评 此题是几何变换综合题,主要考查了等式的性质,等腰直角三角形的判定,垂直的判定方法,利用两个角互余和相等的角,得出角相等或互余,是解本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
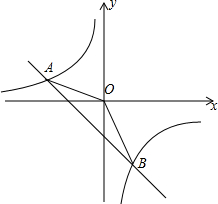 如图,一次函数y=kx-1的图象与反比例函数$y=\frac{m}{x}$的图象相交于A、
如图,一次函数y=kx-1的图象与反比例函数$y=\frac{m}{x}$的图象相交于A、查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
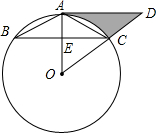 如图,⊙O为△ABC的外接圆,AB=AC,AD∥BC交OC的延长线于点D.
如图,⊙O为△ABC的外接圆,AB=AC,AD∥BC交OC的延长线于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx-75,其图象如图所示.
某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx-75,其图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com