
分析 (1)根据二次项系数非负结合根的判别式△>0,即可得出关于k的一元一次不等式组,解之即可得出k的取值范围;
(2)由(1)的结论可找出k值,将其代入原方程中利用公式法解一元二次方程,即可得出结论.
解答 解:(1)∵关于x的一元二次方程kx2-(k-1)x+$\frac{1}{4}$k=0有两个不相等的实数根,
∴$\left\{\begin{array}{l}{k≠0}\\{△=[-(k-1)]^{2}-4k•\frac{1}{4}k>0}\end{array}\right.$,
解得:k<$\frac{1}{2}$且k≠0.
(2)∵k<$\frac{1}{2}$且k≠0,
∴k取最大整数时k=-1,此时原方程为x2-2x+$\frac{1}{4}$=0,
解得:x1=1+$\frac{\sqrt{3}}{2}$,x2=1-$\frac{\sqrt{3}}{2}$.
点评 本题考查了根的判别式、一元二次方程的定义以及公式法解一元二次方程,解题的关键是:(1)根据二次项系数非负结合根的判别式△>0,列出关于k的一元一次不等式组;(2)熟练掌握公式法解一元二次方程的应用.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案科目:初中数学 来源: 题型:解答题
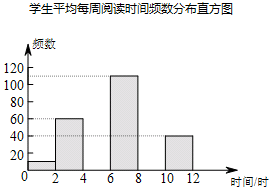 阅读下列材料:
阅读下列材料:| 平均每周阅读时间x(时) | 频数 | 频率 |
| 0≤x<2 | 10 | 0.025 |
| 2≤x<4 | 60 | 0.150 |
| 4≤x<6 | a | 0.200 |
| 6≤x<8 | 110 | b |
| 8≤x<10 | 100 | 0.250 |
| 10≤x<12 | 40 | 0.100 |
| 合计 | 400 | 1.000 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
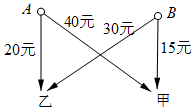 我县黄泛区农场有A、B两个果园,分别收获水果380件,320件,现需把这些水果全部运往甲、乙两个销售点,每件运费如图所示.现甲销售点需水果400件,乙销售点需水果300件.
我县黄泛区农场有A、B两个果园,分别收获水果380件,320件,现需把这些水果全部运往甲、乙两个销售点,每件运费如图所示.现甲销售点需水果400件,乙销售点需水果300件.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
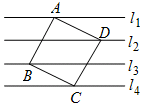 如图,已知直线l1∥l2∥l3∥l4,且相邻两条平行直线间的距离都是d,如果正方形ABCD的四个顶点分别在四条直线上,且面积都是1,则d=$\frac{\sqrt{5}}{5}$.
如图,已知直线l1∥l2∥l3∥l4,且相邻两条平行直线间的距离都是d,如果正方形ABCD的四个顶点分别在四条直线上,且面积都是1,则d=$\frac{\sqrt{5}}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
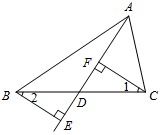 完成下面的证明:
完成下面的证明:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com