
【题目】寻找公式,求代数式的值:从2开始,连续的的偶数相加,它们的和的情况如下表:

(1)根据上面的等式,你能发现当n个连续的的偶数相加时,它们的和S=2+4+6+8+……+2n= .
(2)并按照此规律计算:①2+4+6+……300的值;②162+164+166+……+400的值.
【答案】(1)n(n+1);(2)①22650;②33720.
【解析】
(1)观察所给的算式,找出其中的规律,用含n的式子表示其中的规律;
(2)依据规律进行计算即可.
(1)∵1个最小的连续偶数相加时,S=1×(1+1),
2个最小的连续偶数相加时,S=2×(2+1),
3个最小的连续偶数相加时,S=3×(3+1),
…
∴n个最小的连续偶数相加时,S=n(n+1);
(2)①2+4+6+…+300=150×(150+1)=22650;
②162+164+166+…+400,
=(2+4+6+…+400)(2+4+6+…+160),
=200×20180×81,
=402006480,
=33720.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC和△BDE都是等边三角形。下列结论:① AE=CD;②BF=BG;③BH平分∠AHD;④∠AHC=60°,⑤△BFG是等边三角形;⑥ FG∥AD。其中正确的有_______个.
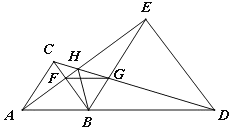
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形纸片ABCD中,AB=8,将纸片折叠,折痕的一个端点F在边AD上,另一个端点G在边BC上,顶点B的对应点为E.
(1)如图(1),当顶点B的对应点E落在边AD上时.
①连接BF,试判断四边形BGEF是怎样的特殊四边形,并说明理由;
②若BG=10,求折痕FG的长;
(2)如图(2),当顶点B的对应点E落在长方形内部,E到AD的距离为2,且BG=10时,求AF的长.
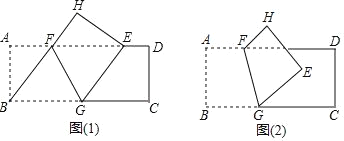
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,E是BC边上一点,F是BA延长线上一点,AF=CE,连接BD,EF,FG平分∠BFE交BD于点G.
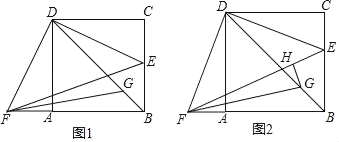
(1)求证:△ADF≌△CDE;
(2)求证:DF=DG;
(3)如图2,若GH⊥EF于点H,且EH=![]() FH,设正方形ABCD的边长为x,GH=y,求y与x之间的关系式.
FH,设正方形ABCD的边长为x,GH=y,求y与x之间的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,△ABC与△DEF关于点O成中心对称,△ABC与△DEF的顶点均在格点上.
(1)在图中直接画出O点的位置;
(2)若以O点为平面直角坐标系的原点,线段AD所在的直线为y轴,过点O垂直AD的直线为x轴,此时点B的坐标为(﹣2,2),请你在图上建立平面直角坐标系,并回答下面的问题:将△ABC先向右平移4个单位长度,再向下平移2个单位长度,得到△A1B1C1,请画出△A1B1C1,并直接写出点B1的坐标.
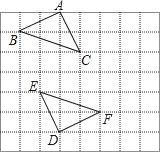
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点D,E是位于AB两侧的半圆AB上的动点,射线DC切⊙O于点D.连接DE,AE,DE与AB交于点P,F是射线DC上一动点,连接FP,FB,且∠AED=45°.
(1)求证:CD∥AB;
(2)填空:
①若DF=AP,当∠DAE=_________时,四边形ADFP是菱形;
②若BF⊥DF,当∠DAE=_________时,四边形BFDP是正方形.
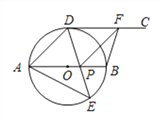
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校部分师生要去外地参加夏令营活动,车站提出两种车票价格优惠方案供学校选择:第一种方案是教师按原价付款,学生按原价的75%付款;第二种方案是师生都按原价的80%付款.已知该校有5名教师和x名学生参加此次夏令营活动,车票原价为100元/张.
(1)分别写出两种方案的购票款(列代数式并化简)
(2)如果两种方案的付款相同,那么参加夏令营的学生有多少人?
(3)当参加夏令营的学生人数为![]() 名时,试说明选择哪一种方案购票省钱?
名时,试说明选择哪一种方案购票省钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com