

分析 (1)根据对称的性质得到BP=BF,由等腰三角形的性质得到∠PBF=2∠ABP,同理DQ=DH,∠HDB=2∠CDB,然后根据全等三角形的判定定理即可得到结论;
(2)由对称的性质得到∠EDA=∠PDA,同理∠PDC=∠HDC,由四边形ABCD是矩形,得到∠ADC=90°,于是得到结论;根据全等三角形的性质得到∠PBF=∠HDQ,根据平行线的性质即可得到结论;通过全等三角形的性质得到∠AFB=∠APB=90°,同理∠DHG=90°,于是得到四边形EFGH是矩形,连接AC,由对称的性质得AP=AE=AF,推出四边形ACHE是平行四边形,得到AC=HE,AC∥HE,等量代换得到结论;当③④同时成立时,EFGH为正方形,于是得到⑤错误;
(3)作A作AM⊥BD于点M,根据三角形的面积公式得到AM=4.8,由(2)知,AP=$\frac{1}{2}$BD=5,根据勾股定理得到PM=$\sqrt{A{P}^{2}-A{M}^{2}}$=1.4,设AC与BD相交于点O,由等腰三角形的性质得到OP=2PM=2.8,即可得到结论.
解答  解:(1)∵点P、F关于AB对称,
解:(1)∵点P、F关于AB对称,
∴BP=BF,
∴∠PBF=2∠ABP,
同理DQ=DH,∠HDB=2∠CDB,
∵BP=DQ,
∴BF=DH,
∵CD∥AB,
∴∠ABD=∠CDB,
∴∠FBD=∠HDB,
在△BFP与△DHQ中,$\left\{\begin{array}{l}{DH=BF}\\{∠HDB=∠FBD}\\{DQ=BP}\end{array}\right.$,
∴△BFP≌△DHQ;
(2)①②③④,
理由:∵P、E关于AD对称,
∴∠EDA=∠PDA,同理∠PDC=∠HDC,
∵四边形ABCD是矩形,
∴∠ADC=90°,
∴∠EDH=180°,
∴点E、D、H三点共线;故①正确;
由(1)证得△BFP≌△DHQ,
∴∠PBF=∠HDQ,
∴EH∥FG,
故②正确;
∵点P、F关于AB对称,
∴BP=BF,AP=AF,
在△ABP与△ABF中,$\left\{\begin{array}{l}{AP=AF}\\{AB=AB}\\{BP=BF}\end{array}\right.$,
∴△ABP≌△ABF,
∴∠AFB=∠APB,
∵AP⊥BD,
∴∠AFB=90°,同理∠DHG=90°,
∵EH∥FG,
∴∠HGF=90°,
∴四边形EFGH是矩形,故③正确;
如图1,连接AC,由对称的性质得AP=AE=AF,
∴A为EF的中点,同理C为HG的中点,
∵四边形EFGH是菱形,
∴AE=CH,AE∥CH,
∴四边形ACHE是平行四边形,
∴AC=HE,AC∥HE,
∵AC=BD,∴BD=EF,
∵EF=2AP,∴BD=2AP,故④正确;
当③④同时成立时,EFGH为正方形,故⑤错误;
故答案为:①②③④;
(3)∵AB=8,AD=6,∴BD=10,
如图2,作A作AM⊥BD于点M ,
,
∵S△ABD=$\frac{1}{2}$AD•AB=$\frac{1}{2}$BD•AM,
∴AM=4.8,
由(2)知,AP=$\frac{1}{2}$BD=5,
∴PM=$\sqrt{A{P}^{2}-A{M}^{2}}$=1.4,
设AC与BD相交于点O,AO=$\frac{1}{2}$BD=AP,
∴△OAP为等腰三角形,M为OP中点,
∴OP=2PM=2.8,
∵BP=DQ,
∴OQ=OP=2.8,
∴PQ=5.6.
点评 本题考查了轴对称的性质,全等三角形的判定和性质,矩形的性质,菱形的性质,平行线的判定和性质,熟练掌握各定理是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
 如图,已知E,F,G,H分别为正方形ABCD各边上的动点,且始终保持AE=BF=CG=DH,点M,N,P,Q分别是EH、EF、FG、HG的中点.当AE从小于BE的变化过程中,若正方形ABCD的周长始终保持不变,则四边形MNPQ的面积变化情况是( )
如图,已知E,F,G,H分别为正方形ABCD各边上的动点,且始终保持AE=BF=CG=DH,点M,N,P,Q分别是EH、EF、FG、HG的中点.当AE从小于BE的变化过程中,若正方形ABCD的周长始终保持不变,则四边形MNPQ的面积变化情况是( )| A. | 一直增大 | B. | 一直减小 | C. | 先增大后减小 | D. | 先减小后增大 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠ACB=90°,△ABC绕点A旋转得到△ADE(E与C对应,D与B对应),连接EC并延长交BD于F.
如图,在Rt△ABC中,∠ACB=90°,△ABC绕点A旋转得到△ADE(E与C对应,D与B对应),连接EC并延长交BD于F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
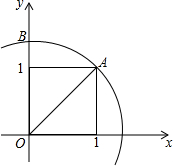 如图,平面直角坐标中,以x轴上一个单位长度为边长画一个正方形,以原点为圆心,正方形的对角线OA为半径画弧,与y轴正半轴的交点B表示的坐标是(0,$\sqrt{2}$).
如图,平面直角坐标中,以x轴上一个单位长度为边长画一个正方形,以原点为圆心,正方形的对角线OA为半径画弧,与y轴正半轴的交点B表示的坐标是(0,$\sqrt{2}$).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com