
分析 将方程x2+a-$\frac{4}{x}$=0(a>0)得解看成两函数y=x2+a与y=$\frac{4}{x}$的交点问题,先找出函数y=x2和y=$\frac{4}{x}$的交点坐标,根据平移的性质即可得出方程x2+a-$\frac{4}{x}$=0(a>0)的解为x=1,将其代入原方程中即可求出a值.
解答 解:将方程x2+a-$\frac{4}{x}$=0(a>0)得解看成两函数y=x2+a与y=$\frac{4}{x}$的交点问题,画出两函数的图象如图所示.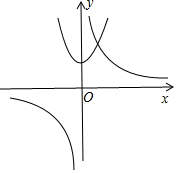
当x2-$\frac{4}{x}$=0时,解得:x=$\root{3}{4}$,
而y=x2+a(a>0)可以看成把函数y=x2的图象往上平移a个单位,
∵1<$\root{3}{4}$<2,关于x的方程x2+a-$\frac{4}{x}$=0(a>0)只有一个整数解,
∴x=1.
将x=1代入方程程x2+a-$\frac{4}{x}$=0中,得1+a-4=0,
解得:a=3.
故答案为:3.
点评 本题考查了二次函数的图象以及反比例函数的图象,解题的关键是求出方程x2+a-$\frac{4}{x}$=0(a>0)的整数解为x=1.本体属于中档题,难度不大,解决该题型题目时,将方程的解转化成函数图象交点的问题,画出函数图象,利用数形结合即可得出结论.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:选择题
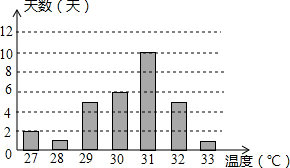 小慧将今年五月深圳每天的最高气温情况绘制成条形统计图,根据图中信息,五月最高气温的众数与中位数分别为( )
小慧将今年五月深圳每天的最高气温情况绘制成条形统计图,根据图中信息,五月最高气温的众数与中位数分别为( )| A. | 33,30 | B. | 31,30 | C. | 31,31 | D. | 31,33 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 2015年8月17日大河网报道,大学生身体素质不如中学生,王老师为了解该校八年级500名学生的体能情况,随机抽取了50名学生,测试了1分钟仰卧起坐的次数,并将数据绘制成如图所示的频数分布直方图(注:15~20包括15,不包括20,下同).已知第1组的频数为2,第2组的频率为20%,则这次测试中合格(1分钟仰卧起坐的次数大于等于25)的学生有(
2015年8月17日大河网报道,大学生身体素质不如中学生,王老师为了解该校八年级500名学生的体能情况,随机抽取了50名学生,测试了1分钟仰卧起坐的次数,并将数据绘制成如图所示的频数分布直方图(注:15~20包括15,不包括20,下同).已知第1组的频数为2,第2组的频率为20%,则这次测试中合格(1分钟仰卧起坐的次数大于等于25)的学生有(| A. | 34名 | B. | 36名 | C. | 38名 | D. | 40名 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 日期 | 5月1日 | 5月2日 | 5月3日 | 5月4日 | 5月5日 | 5月6日 | 5月7日 |
| 人数(万人) | 1.2 | 2 | 1.2 | 2.5 | 2 | 2 | 0.6 |
| A. | 1.2,2 | B. | 2,2.5 | C. | 2,2 | D. | 1.2,2.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com