
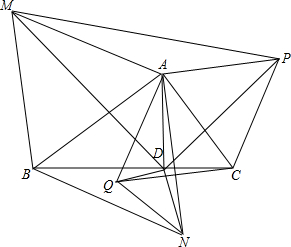
 AD是Rt△ABC的垂线,以AB为边长,分别向内,外做正三角形ABN、ABM,以AC为边长,分别向内、外作正三角形ACQ、ACP,连接MD、ND、PD、QD、MP、QN,求证:△MPD相似于△NQD.
AD是Rt△ABC的垂线,以AB为边长,分别向内,外做正三角形ABN、ABM,以AC为边长,分别向内、外作正三角形ACQ、ACP,连接MD、ND、PD、QD、MP、QN,求证:△MPD相似于△NQD. 分析 由直角三角形的性质得出∠CAD=∠ABD,证出△CAD∽△ABD,得出$\frac{AD}{AC}=\frac{BD}{AB}$,再由等边三角形的性质得出$\frac{AD}{AP}=\frac{BD}{BM}$,证出∠PAD=∠MBD,得出△PAD∽△MBD,得出$\frac{PD}{MD}=\frac{PA}{MB}=\frac{AC}{AB}$,∠PDA=∠MDB,再证明△ADQ∽△BDN,得出$\frac{DQ}{DN}=\frac{AD}{BD}=\frac{AC}{AB}$,∠ADQ=∠BDN,证出∠QDN=∠PDM,由$\frac{PD}{MD}=\frac{DQ}{DN}$,即可得出结论.
解答 证明:AD是Rt△ABC的垂线,
∴AD⊥BC,∠CAD+∠BAD=90°,∠ABD+∠BAD=90°,
∴∠CAD=∠ABD,
∴△CAD∽△ABD,
∴$\frac{AD}{AC}=\frac{BD}{AB}$,
∵△ACP、△ABM是等边三角形,
∴AP=AC,BM=AB,
∴$\frac{AD}{AP}=\frac{BD}{BM}$,
∵∠PAD=∠PAC+∠CAD=60°+∠CAD,∠MBD=∠ABM+∠ABD=60°+∠ABD,
∴∠PAD=∠MBD,
∴△PAD∽△MBD,
∴$\frac{PD}{MD}=\frac{PA}{MB}=\frac{AC}{AB}$,∠PDA=∠MDB,
∴∠PDM=∠PDA+∠ADM=∠MDB+∠ADM=90°,
∵∠CAQ=60°=∠ABN,∠CAD=∠ABD,
∴∠DAQ=∠DBN,
∵$\frac{AQ}{AD}=\frac{AC}{AD}=\frac{BD}{AB}=\frac{BD}{BN}$,
∴△ADQ∽△BDN,
∴$\frac{DQ}{DN}=\frac{AD}{BD}=\frac{AC}{AB}$,∠ADQ=∠BDN,
∴∠QDN=∠BDN-∠BDQ=∠ADQ-∠BDQ=90°,
∴∠QDN=∠PDM,
∵$\frac{PD}{MD}=\frac{DQ}{DN}$,
∴△MPD∽△NQD.
点评 本题考查了相似三角形的判定与性质、直角三角形的性质、等边三角形的性质等知识;熟练掌握等边三角形的性质,证明三角形相似是解决问题的关键.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)已知关于x的一元二次方程(a+c)x2+bx+(a-c)=0,其中a,b,c分别为△ABC的边长.若(a,b),c分别为⊙M的圆心坐标和半径,则称⊙M为△ABC的“伴侣圆”.
(1)已知关于x的一元二次方程(a+c)x2+bx+(a-c)=0,其中a,b,c分别为△ABC的边长.若(a,b),c分别为⊙M的圆心坐标和半径,则称⊙M为△ABC的“伴侣圆”.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com