
阅读材料:若a,b都是非负实数,则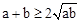 .当且仅当a=b时,“=”成立.
.当且仅当a=b时,“=”成立.
证明:∵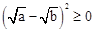 ,∴
,∴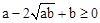 .
.
∴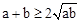 .当且仅当a=b时,“=”成立.
.当且仅当a=b时,“=”成立.
举例应用:已知x>0,求函数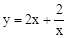 的最小值.
的最小值.
解: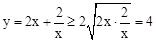 .当且仅当
.当且仅当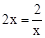 ,即x=1时,“=”成立.
,即x=1时,“=”成立.
当x=1时,函数取得最小值,y最小=4.
问题解决:汽车的经济时速是指汽车最省油的行驶速度.某种汽车在每小时70~110公里之间行驶时(含70公里和110公里),每公里耗油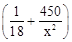 升.若该汽车以每小时x公里的速度匀速行驶,1小时的耗油量为y升.
升.若该汽车以每小时x公里的速度匀速行驶,1小时的耗油量为y升.
(1)求y关于x的函数关系式(写出自变量x的取值范围);
(2)求该汽车的经济时速及经济时速的百公里耗油量(结果保留小数点后一位).
科目:初中数学 来源: 题型:阅读理解
| ab |
| a |
| b |
| ab |
| ab |
| 2 |
| x |
| 2 |
| x |
2x•
|
| 2 |
| x |
| 1 |
| 18 |
| 450 |
| x2 |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
阅读材料:若a,b都是非负实数,则![]() .当且仅当a=b时,“=”成立.
.当且仅当a=b时,“=”成立.
证明:∵![]() ,∴
,∴![]() .
.
∴![]() .当且仅当a=b时,“=”成立.
.当且仅当a=b时,“=”成立.
举例应用:已知x>0,求函数![]() 的最小值.
的最小值.
解:![]() .当且仅当
.当且仅当![]() ,即x=1时,“=”成立.
,即x=1时,“=”成立.
当x=1时,函数取得最小值,y最小=4.
问题解决:汽车的经济时速是指汽车最省油的行驶速度.某种汽车在每小时70~110公里之间行驶时(含70公里和110公里),每公里耗油![]() 升.若该汽车以每小时x公里的速度匀速行驶,1小时的耗油量为y升.
升.若该汽车以每小时x公里的速度匀速行驶,1小时的耗油量为y升.
(1)求y关于x的函数关系式(写出自变量x的取值范围);
(2)求该汽车的经济时速及经济时速的百公里耗油量(结果保留小数点后一位).
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
阅读材料:若a,b都是非负实数,则![]() .当且仅当a=b时,“=”成立.
.当且仅当a=b时,“=”成立.
证明:∵![]() ,∴
,∴![]() .
.
∴![]() .当且仅当a=b时,“=”成立.
.当且仅当a=b时,“=”成立.
举例应用:已知x>0,求函数![]() 的最小值.
的最小值.
解:![]() .当且仅当
.当且仅当![]() ,即x=1时,“=”成立.
,即x=1时,“=”成立.
当x=1时,函数取得最小值,y最小=4.
问题解决:汽车的经济时速是指汽车最省油的行驶速度.某种汽车在每小时70~110公里之间行驶时(含70公里和110公里),每公里耗油![]() 升.若该汽车以每小时x公里的速度匀速行驶,1小时的耗油量为y升.
升.若该汽车以每小时x公里的速度匀速行驶,1小时的耗油量为y升.
(1)求y关于x的函数关系式(写出自变量x的取值范围);
(2)求该汽车的经济时速及经济时速的百公里耗油量(结果保留小数点后一位).
查看答案和解析>>
科目:初中数学 来源:2013年山东省济宁市中考数学试卷(解析版) 题型:解答题
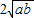 .当且仅当a=b时,“=”成立.
.当且仅当a=b时,“=”成立.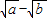 )2≥0,∴a-
)2≥0,∴a-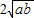 +b≥0.
+b≥0.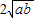 .当且仅当a=b时,“=”成立.
.当且仅当a=b时,“=”成立.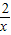 的最小值.
的最小值.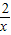 ≥
≥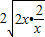 =4.当且仅当2x=
=4.当且仅当2x=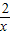 ,即x=1时,“=”成立.
,即x=1时,“=”成立.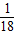 +
+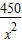 )升.若该汽车以每小时x公里的速度匀速行驶,1小时的耗油量为y升.
)升.若该汽车以每小时x公里的速度匀速行驶,1小时的耗油量为y升.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com