
【题目】关于x的一元二次方程![]() 有两个不相等的实数根
有两个不相等的实数根![]() 、
、![]() .(1)求实数k的取值范围.
.(1)求实数k的取值范围.
(2)若方程的两个实数根![]() 、
、![]() 满足
满足![]() ,求k的值.
,求k的值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)由方程的系数结合根的判别式即可得出关于k的一元一次不等式,解之即可得出实数k的取值范围;
(2)由根与系数的关系可得x1+x2=﹣(2k+1)、x1x2=k2+1,结合x1+x2=-x1x2即可得出关于k的一元二次方程,解之即可得出k值,再根据k>![]() 即可确定k的值.
即可确定k的值.
试题解析:解:(1)∵关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不相等的实数根,∴△=(2k+1)2﹣4(k2+1)=4k﹣3>0,解得:k>![]() ,∴实数k的取值范围为k>
,∴实数k的取值范围为k>![]() .
.
(2)由根与系数的关系,得:x1+x2=﹣(2k+1),x1x2=k2+1,∵x1+x2=-x1x2,∴﹣(2k+1)=-(k2+1),∴k2﹣2k=0.解得:k=0或k=2,∵k>![]() ,∴k=2.
,∴k=2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(1)甲、乙、丙、丁四人做传球游戏:第一次由甲将球随机传给乙、丙、丁中的某一人,从第二次起,每一次都由持球者将球再随机传给其他三人中的某一人.求第二次传球后球回到甲手里的概率.(请用“画树状图”的方式给出分析过程)
(2)如果甲跟另外n(n≥2)个人做(1)中同样的游戏,那么,第三次传球后球回到甲手里的概率是 (请直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从2007年4月18日零点起,铁路将实施第六次大提速,届时“子弹头”动力组列车的速度将大大提高.若有一普通列车长为140米,“子弹头”动力组列车长为110米,两列车若同向而行,两车交汇的时间为9秒,若两列车相向而行,两车交汇的时间为3秒,求“子弹头”动力组列车和普通列车的速度分别为多少?若设“子弹头”动力组列车的速度为x米/秒,普通列车速度为y米/秒,则可列出方程组为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市政府2007年准备投入一定资金加大对主城区的改造力度,但又不影响对教育及其他方面的投入.下面是市规划局等部门提供的信息:
2002年 | 2003年 | 2004年 | 2005年 | |
政府划拨资金 | 1.2 | 1.4 | 1.5 | 1.6 |
招商引进资金 | 5.8 | 6.1 | 6.25 | 6.4 |
①2007年用于主城区改造的资金不超过2007年教育投入的3倍.
②计划2007年比2006年的教育投入多0.5亿元,这样两年的教育投入之比为6:5.
③用于主城区改造的资金一部分由政府划拨,其余来源于招商引资.据分析发现,招商所引资金与政府划拨的资金始终满足某种函数关系.(如下表所示)
政府划拨资金与招商引进资金对照表:(单位:亿元)
④2007年招商引资的投资者从2008年起每年共可获得0.67亿元的回报,估计2007年招商引进的资金至少10年方可收回.
(1)该市政府2006年对教育的投入为多少亿元?
(2)求招商引进资金y(单位:亿元)与财政划拨部分x(单位:亿元)之间的函数关系式;
(3)求2007年该市在主城区改造中财政划拨的资金的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三角形DEF是三角形ABC经过某种变换得到的图形,点A与点D、点B与点E、点C与点F分别是对应点.观察点与点的坐标之间的关系,解答下列问题:
(1)分别写出点A与点D、点B与点E、点C与点F的坐标,并说出三角形DEF是由三角形ABC经过怎样的变换得到的;
(2)若点Q(a+3,4-b)是点P(2a,2b-3)通过上述变换得到的,求a-b的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某天在南印度洋海域有两艘自西向东航行的搜救船A、B,B船在A船的正东方向,且两船保持40海里的距离.某一时刻两船同时测得在A的东北方向,B的北偏东15°方向有一疑似物C,求此时疑似物C与搜救船A、B的距离各是多少?(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应国家节能减排的号召,鼓励居民节约用电,各省市先后出台了“阶梯价格”制度,如表中是某市的电价标准(每月)
阶梯 | 电量x(单位:度) | 电费价格(单位:元/度) |
一档 | 0<x≤180 | a |
二档 | 180<x≤400 | b |
三档 | x>400 | 0.95 |
(1)已知陈女士家三月份用电256度,缴纳电费154.56元,四月份用电318度,缴纳电费195.48元请你根据以上数据,求出表格中的a,b的值.
(2)5月份开始用电增多,陈女士缴纳电费280元,求陈女士家5月份的用电量.
查看答案和解析>>
科目:初中数学 来源: 题型:
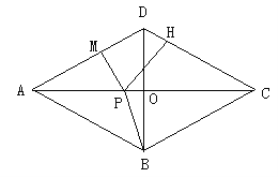
【题目】(13分)如图所示,四边形![]() 中,
中, ![]() 于点
于点![]() ,
, ![]() ,
, ![]() ,点
,点![]() 为线段
为线段![]() 上的一个动点。
上的一个动点。
(1)求证: ![]() 。
。
(2)过点![]() 分别作
分别作![]() 于
于![]() 点,作
点,作![]() 于
于![]() 点。
点。
① 试说明![]() 为定值。
为定值。
② 连结![]() ,试探索:在点
,试探索:在点![]() 运动过程中,是否存在点
运动过程中,是否存在点![]() ,使
,使![]() 的值最小。若存在,请求出该最小值;若不存在,请说明理由。
的值最小。若存在,请求出该最小值;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】威丽商场销售A、B两种商品,售出1件A种商品和4件B种商品所得利润为600元;售出3件A种商品和5件B种商品所得利润为1100元.
(1)求每件A种商品和每件B种商品售出后所得利润分别为多少元?
(2)由于需求量大,A、B两种商品很快售完,威丽商场决定再一次购进A、B两种商品共34件,如果将这34件商品全部售完后所得利润不低于4000元,那么威丽商场至少需购进多少件A种商品?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com