

分析 (1)根据点Q移动速度是点P速度的3倍及P移动的距离为x,得到BQ=3x,由BQ-BP表示出PQ,即为正方形边长,过D作DE垂直于BC,求出DE与CE的长,利用锐角三角函数定义求出tan∠BCD的值即可;
(2)如图1所示,当M在边CD上时,表示出MQ与CQ,根据tan∠BCD的值列出关于x的方程,求出方程的解即可得到x的值;
(3)分四种情况考虑:当0<x≤$\frac{9}{7}$时,如图1所示;当$\frac{9}{7}$<x≤1.5时,如图2所示;当1.5<x<3时,如图3所示;当3≤x<9时,如图4所示,分别表示出y与x的关系式即可.
解答 解:(1)根据题意得:BQ=3BP=3x,
∴PQ=BQ-BP=3x-x=2x,即正方形PQMN的边长是2x;
过D作DE⊥BC,
在Rt△DEC中,DE=AB=3,CE=BC-BE=9-3=6,
∴tan∠BCD=$\frac{DE}{CE}$=$\frac{3}{6}$=$\frac{1}{2}$;
故答案为:2x;$\frac{1}{2}$;
(2)如图1所示,当M在边CD上时,可得MQ=PQ=2x,BQ=3x,BP=x,CQ=BC-BQ=9-3x,
在Rt△MQC中,tan∠BCD=$\frac{MQ}{CQ}$=$\frac{2x}{9-3x}$=$\frac{1}{2}$,
解得:x=$\frac{9}{7}$;
(3)当0<x≤$\frac{9}{7}$时,如图1所示,正方形PQMN与梯形ABCD的重叠部分面积为y=(2x)2=4x2;
当$\frac{9}{7}$<x≤1.5时,如图2所示,正方形PQMN与梯形ABCD的重叠部分为五边形EFQPN,过E作EM⊥BC,
由题意得:BP=x,EM=PQ=2x,CM=2EM=4x,则BM=9-4x,
∴PM=NE=BM-BP=9-4x-x=9-5x,
∵tan∠MEF=tan∠BCD=$\frac{1}{2}$,
∴EM=2x-(9-5x)=7x-9,FM=$\frac{1}{2}$(7x-9),
此时重合面积为y=(2x)2-$\frac{1}{4}$(7x-9)2=-$\frac{33}{4}$x2+$\frac{63}{2}$x-$\frac{81}{4}$;
当1.5<x<3时,如图3所示,过D作DE⊥BC,
可得DE=FP=3,BP=x,PE=FD=3-x,PQ=2x,
∵tan∠GCD=$\frac{1}{2}$,
∴EQ=PQ-PE=2x-(3-x)=3x-3,CQ=9-3x,DG=$\frac{1}{2}$(9-3x),
此时重叠部分面积y=3(3-x)+$\frac{1}{2}$(3x-3)[$\frac{1}{2}$(9-3x)+3]=-$\frac{9}{4}$x2+$\frac{21}{2}$x-$\frac{45}{4}$;
当3≤x<9时,如图4所示,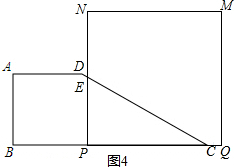
由题意得:BP=x,BQ=3x,PQ=2x,BC=9,
∴PC=BC-BP=9-x,
∵tan∠ECP=$\frac{1}{2}$,
∴EP=$\frac{1}{2}$(9-x),
此时重叠部分面积y=$\frac{1}{4}$(9-x)2=$\frac{1}{4}$x2-$\frac{9}{2}$x+$\frac{81}{4}$.
点评 此题属于四边形综合题,涉及的知识有:锐角三角函数定义,正方形,梯形,三角形面积的计算,利用了数形结合及分类讨论的思想,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
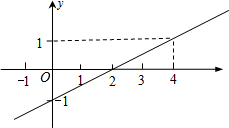 已知一次函数y=$\frac{1}{2}$x-1的图象如图所示,下列正确的有( )个.
已知一次函数y=$\frac{1}{2}$x-1的图象如图所示,下列正确的有( )个.| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
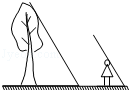 某数学兴趣小组利用太阳光测量一棵树的高度(如图),在同一时刻,测得树的影长为4.8米,小明的影长为1.2米,已知小明的身高为1.5米,则树高为6米.
某数学兴趣小组利用太阳光测量一棵树的高度(如图),在同一时刻,测得树的影长为4.8米,小明的影长为1.2米,已知小明的身高为1.5米,则树高为6米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在等腰三角形ABC中,AB=AC,D是AB边上一点,以CD为一边,向上作等腰△DCE,使△EDC∽△ABC,连AE,求证:
如图,在等腰三角形ABC中,AB=AC,D是AB边上一点,以CD为一边,向上作等腰△DCE,使△EDC∽△ABC,连AE,求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com