试题分析:(1)①根据切线的性质以及直角三角形的性质得出∠EBA的度数即可:
∵半径为2cm的与⊙O边长为2cm的正方形ABCD在水平直线l的同侧,当点A在⊙O上时,过点B作的一条切线BE,E为切点,
∴OB=4,EO=2,∠OEB=90°。
∴∠EBA的度数是:30°。
②利用切线的性质以及矩形的性质和相似三角形的判定和性质得出
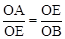
,进而求出OA即可。
如图2,
∵直线l与⊙O相切于点F,∴∠OFD=90°。
∵正方形ADCB中,∠ADC=90°,∴OF∥AD。
∵OF=AD=2,∴四边形OFDA为平行四边形。
∵∠OFD=90°,∴平行四边形OFDA为矩形。∴DA⊥AO。
∵正方形ABCD中,DA⊥AB,O、A、B三点在同一条直线上,∴EA⊥OB。
∵∠OEB=∠AOE,∴△EOA∽△BOE。
∴
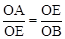
,即
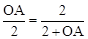
,解得:
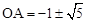
。
∵OA>0,∴
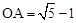
。
(2)设∠MON=n°,得出
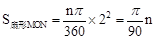
,进而利用函数增减性分析①当N,M,A分别与D,B,O重合时,MN最大,②当MN=DC=2时,MN最小,分别求出即可。
如图3,设∠MON=n°,
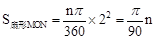
(cm
2)。

∴S随n的增大而增大,当∠MON取最大值时,S
扇形MON最大,当∠MON取最小值时,S
扇形MON最小。
过O点作OK⊥MN于K,∴∠MON=2∠NOK,MN=2NK。
在Rt△ONK中,
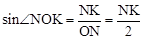
,
∴∠NOK随NK的增大而增大。
∴∠MON随MN的增大而增大。
∴当MN最大时∠MON最大,当MN最小时∠MON最小。
①当N,M,A分别与D,B,O重合时,MN最大,
此时,MN=BD,∠MON=∠BOD=90°,
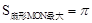
(cm
2)。
②当MN=DC=2时,MN最小,
此时,ON=MN=OM。∴∠NOM=60°。
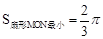
(cm
2)。
∴
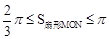
。


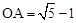
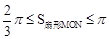
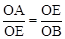 ,进而求出OA即可。
,进而求出OA即可。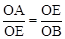 ,即
,即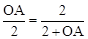 ,解得:
,解得: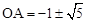 。
。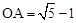 。
。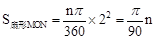 ,进而利用函数增减性分析①当N,M,A分别与D,B,O重合时,MN最大,②当MN=DC=2时,MN最小,分别求出即可。
,进而利用函数增减性分析①当N,M,A分别与D,B,O重合时,MN最大,②当MN=DC=2时,MN最小,分别求出即可。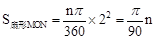 (cm2)。
(cm2)。
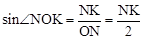 ,
,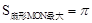 (cm2)。
(cm2)。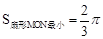 (cm2)。
(cm2)。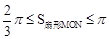 。
。


 ,求EF的长.
,求EF的长.
 时,求弦ED的长.
时,求弦ED的长.