
【题目】已知关于![]() ,
,![]() 的方程组
的方程组![]() ,则下列结论中:①当
,则下列结论中:①当![]() 时,方程组的解是
时,方程组的解是![]() ;②当
;②当![]() ,
,![]() 的值互为相反数时,
的值互为相反数时,![]() ;③不存在一个实数
;③不存在一个实数![]() 使得
使得![]() ;④若
;④若![]() ,则
,则![]() 正确的个数有( )
正确的个数有( )
A. 1个B. 2个C. 3个D. 4个
科目:初中数学 来源: 题型:
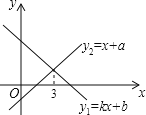
【题目】一次函数![]() 与
与![]() 的图象如图,则下列结论①
的图象如图,则下列结论①![]() ②
②![]() ,且
,且![]() 的值随着
的值随着![]() 值的增大而减小.③关于
值的增大而减小.③关于![]() 的方程
的方程![]() 的解是
的解是![]() ④当
④当![]() 时,
时,![]() ,其中正确的有___________.(只填写序号)
,其中正确的有___________.(只填写序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人买了相同数量的信封和信笺,甲每发一封信都只用1张信笺,乙每发一封信都要用3张信笺,结果甲用掉了所有的信封,但余下50张信笺,而乙用掉了所有的信笺,但余下50个信封.
(1)求甲乙两人各买的信封和信笺的数量分别为多少?
(2)若甲乙两人每发出一封信需邮费5元,求甲乙各用去多少元邮费?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:BC∥OA,∠B=∠A=120°,试回答下列问题:
(1)如图1所示,求证:OB∥AC;

(2)如图2,若点E、F在BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF,则∠EOC的度数是______;

(3)在(2)的条件下,若平行移动AC,其它条件不变,如图3,则∠OCB:∠OFB的值是______.
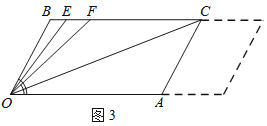
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大家见过形如x+y=z,这样的三元一次方程,并且知道x=3,y=4,z=7就是适合该方程的一个正整数解,法国数学家费尔马早在17世纪还研究过形如x2+y2=z2的方程.
(1)请写出方程x2+y2=z2的两组正整数解: .
(2)研究直角三角形和勾股数时,我国古代数学专著(九章算术)给出了如下数:a=![]() (m2﹣n2),b=mn,c=
(m2﹣n2),b=mn,c=![]() (m2+n2),(其中m>n,m,n是奇数),那么,以a,b,c为三边的三角形为直角三角形,请你加以验证.
(m2+n2),(其中m>n,m,n是奇数),那么,以a,b,c为三边的三角形为直角三角形,请你加以验证.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A(﹣3,0),点B是x轴上异于点A一动点,设B(x,0),以AB为边在x轴的上方作正方形ABCD.

(1)如图(1),若点B(1,0),则点D的坐标为 ;
(2)若点E是AB的中点,∠DEF=90°,且EF交正方形外角的平分线BF于F.
①如图(2),当x>0时,求证:DE=EF;
②若点F的纵坐标为y,求y关于x的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC是等边三角形,点A与点D的坐标分别是A(4,0),D(10,0).
(1)如图①,当点C与点O重合时,求直线BD的表达式;
(2)如图②,点C从点O沿y轴向下移动,当以点B为圆心,AB为半径的☉B与y轴相切(切点为C)时,求点B的坐标;
(3)如图③,点C从点O沿y轴向下移动,当点C的坐标为C(0,-2![]() )时,求∠ODB的正切值.
)时,求∠ODB的正切值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公园的门票每张20元,一次性使用.考虑到人们的不同需求,也为了吸引更多的游客,该公园除保留原来的售票方法外,还推出了一种“购买个人年票”(个人年票从购买日起,可供持票者使用一年)的售票方法.年票分A,B,C三类,A类年票每张240元,持票进入该园区时,无需再购买门票;B类年票每张120元,持票者进入该园区时,需再购买门票,每次4元;C类年票每张80元,持票者进入该园区时,需再购买门票,每次6元.
(1)如果只能选择一种购买年票的方式,并且计划在一年中花费160元在该公园的门票上,通过计算,找出可进入该园区次数最多的方式.
(2)一年中进入该公园超过多少次时,A类年票比较合算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com