
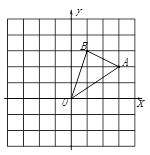
【题目】如图,在边长为1的正方形组成的网格中建立直角坐标系,△AOB的顶点均在格点上,点O为原点,点A、B的的坐标分别为A(3,2)、B(1,3).
⑴.请画出将△AOB向左平移3个单位后得到的图形△A1OB1,点B1的坐标为 ;
⑵.请画出将△AOB关于原点O成对称的图形△A2OB2,点A2的坐标为 ;
⑶.在x轴上找一点P,使PA+PB的值最小,则P点的坐标为 .
【答案】(1)作图见解析,B1(-2,3);(2)作图见解析,A2(-3,-2);(3)作图见解析,P(2.2,0).
【解析】试题分析:(1)根据平移规律解答;
(2)根据中心对称图形的概念解答;
(3)根据轴对称-最短路径问题解答.
试题解析:(1)将△AOB向左平移3个单位后得到的图形△A1OB1如图所示,
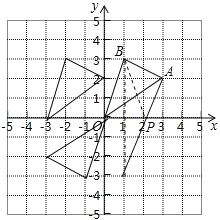
点B1的坐标为(-2,3);
(2)将△AOB关于原点O成对称的图形△A2OB2如图所示,
点A2的坐标为(-3,-2);
(3)作点B关于x轴的对称点B′,连接AB′交x轴于点P,则点P即为所求,
点B′的坐标为(1,-3),
设直线AB′的解析式为:y=kx+b,
![]() ,
,
解得,k=![]() ,b=-
,b=-![]() ,
,
则直线AB′的解析式为:y=![]() x-
x-![]() ,
,
![]() x-
x-![]() =0,
=0,
解得,x=2.2,
则P点的坐标为(2.2,0),


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小明遇到这样一个问题:
如图1,△ABC中,∠A=90°,∠B=30°,点D,E分别在AB,BC上,且∠CDE=90°.当BE=2AD时,图1中是否存在与CD相等的线段?若存在,请找出并加以证明,若不存在,说明理由.
小明通过探究发现,过点E作AB的垂线EF,垂足为F,能得到一对全等三角形(如图2),从而将解决问题.
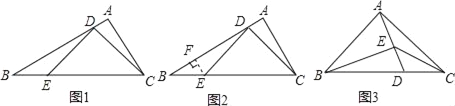
请回答:
(1)小明发现的与CD相等的线段是_____.
(2)证明小明发现的结论;
参考小明思考问题的方法,解决下面的问题:
(3)如图3,△ABC中,AB=AC,∠BAC=90°,点D在BC上,BD=2DC,点E在AD上,且∠BEC=135°,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备购买A、B两种奖品,奖励成绩优异的同学.已知购买1件A奖品和1件B奖品共需18元;购买30件A奖品和20件B奖品共需480元.
(1)A、B两种奖品的单价分别是多少元?
(2)如果学校购买两种奖品共100件,总费用不超过850元,那么最多可以购买A奖品多少件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司招聘人才,对应聘者分别进行阅读能力、专业知识、表达能力三项测试,并将三项测试得分按3:5:2的比例确定每人的最终成绩,现欲从甲乙两选手中录取一人,已知两人的各项测试得分如下表(单位:分)
阅读 | 专业 | 表达 | |
甲 | 93 | 86 | 73 |
乙 | 95 | 81 | 79 |
①请通过相关的计算说明谁将被录用?
②请对落选者今后的应聘提些合理的建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知抛物线y=ax2+bx+c过点A(﹣1,0),且经过直线y=x﹣3与坐标轴的两个交点B、C.
(1)求抛物线的表达式;
(2)若点M在第四象限内且在抛物线上,有OM⊥BC,垂足为D,求点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将两个全等的直角三角形△ABD、△ACE拼在一起(图(1)).令△ABD不动,
(1)若将△ACE绕点A逆时针旋转,连接DE,M是DE的中点,连接MB、MC(图(2)),证明:MB=MC.
(2)若将图(1)中的CE向上平移,∠CAE不变,连接DE,M是DE的中点,连接MB、MC(图(3)),判断MB、MC的数量关系,并说明理由.
(3)在(2)中,若∠CAE的大小改变(图(4)),其他条件不变,则(2)中的MB、MC的数量关系还成立吗?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个三位数,如果把它的个位数字与百位数字交换位置,那么所得的新数比原数小99,且各位数字之和为14,十位数字是个位数字与百位数字之和.求这个三位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级学生准备去购买《英汉词典》一书,此书标价为20元。现A、B两书店都有此书出售,A店按如下方法促销:若只购一本,则按标价销售;若一次性购买多于一本,但不多出20本时,每多购一本,每本销售价在标价的基础上优惠2%(例如买两本,每本价优惠2%;买三本价优惠4%,以此类推);若购买多于20本时,每本售价为12元,B店一律按标价的7折销售;
(1)试分别写出在两书店购此书的总价yA、yB与购本书数x之间的函数关系式.
(2)若某班一次性购买多于20本时,那么去哪家书店购买更合算?为什么?若要一次性购买不多于20本时,先写出y(y=yA-yB)与购书本数x之间的函数关系式,并在图中画出其函数图象,再利用函数图象分析去哪家书店购买更合算.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数 y=kx+b(k≠0)的图象经过点(-1,-5),(2,1)两点.
(1)求 k 和 b 的值;
(2)一次函数 y=kx+b 图象与坐标轴所围成的三角形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com