
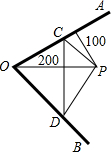
 如图,两条河交汇于O点,夹75°角,旅行家住在P点,离O点200m,离河岸AO100cm.他希望到AO上任一点处欣赏风光,再折到河岸BO上任一点D处眺望景物,然后回到住地,则旅行家最少要走
如图,两条河交汇于O点,夹75°角,旅行家住在P点,离O点200m,离河岸AO100cm.他希望到AO上任一点处欣赏风光,再折到河岸BO上任一点D处眺望景物,然后回到住地,则旅行家最少要走 解:作P点关于AO,BO的对称点P′,P″,连接P″P′即可得出C,D点的位置,连接OP′,OP″,作P′M⊥PO,并延长到点M,作P″M⊥P′M,
解:作P点关于AO,BO的对称点P′,P″,连接P″P′即可得出C,D点的位置,连接OP′,OP″,作P′M⊥PO,并延长到点M,作P″M⊥P′M,| 2 |
| 3 |
| QP′2+ZQ2 |
| ZO2+P″O2 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
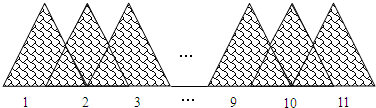 如图,是一块玻璃纸的一部分,它由11个边长为4
如图,是一块玻璃纸的一部分,它由11个边长为4| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
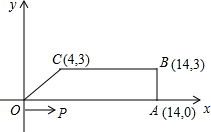 如图,梯形OABC中,O为直角坐标系的原点,A、B、C的坐标分别为A(14,0)、B(14,3)、C(4,3),点P、Q为两动点,同时从原点出发,分别作匀速运动,其中P点沿OA向终点A运动,速度为每秒1个单位;点Q沿OC、CB向终点B运动,速度为每秒2个单位.且当这两点中有一点到达自己的终点时,另一点也停止运动.设运动的时间为t秒.
如图,梯形OABC中,O为直角坐标系的原点,A、B、C的坐标分别为A(14,0)、B(14,3)、C(4,3),点P、Q为两动点,同时从原点出发,分别作匀速运动,其中P点沿OA向终点A运动,速度为每秒1个单位;点Q沿OC、CB向终点B运动,速度为每秒2个单位.且当这两点中有一点到达自己的终点时,另一点也停止运动.设运动的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:
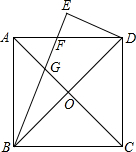 如图,正方形ABCD的对角线AC、BD交于点O,∠ABD的平分线BE交AC于G,交AD于F,且DE⊥BE.
如图,正方形ABCD的对角线AC、BD交于点O,∠ABD的平分线BE交AC于G,交AD于F,且DE⊥BE.| 1 |
| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 一艘轮船在A处,北偏东45°.方向上有一灯塔P,轮船沿着北偏西30°方向航行4小时达到B处,这时灯塔P正好在轮船的正东方向上,已知轮船的航速为25海里/小时,求轮船在B处
一艘轮船在A处,北偏东45°.方向上有一灯塔P,轮船沿着北偏西30°方向航行4小时达到B处,这时灯塔P正好在轮船的正东方向上,已知轮船的航速为25海里/小时,求轮船在B处查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| (n-1)×n |
| 1 |
| 1+2 |
| 1 |
| 1+2+3 |
| 1 |
| 1+2+3+…+n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com