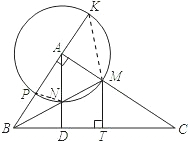
证明:(1)∵BM平分∠ABC,∠BAC=90°,MT⊥BC,
∴AM=MT.
又∵AM=AK,
∴AK=MT.
(2)∵BM平分∠ABC,
∴∠ABM=∠CBM.
∵AM=AN,
∴∠AMN=∠ANM.
又∵∠ANM=∠BND,
∴∠AMN=∠BND.
∵∠BAC=90°,
∴∠ABM+∠AMB=90°.
∴∠CBM+∠BND=90°.
∴∠BDN=90°.
∴AD⊥BC.
(3)连接PN、KM
∵BNM和BPK为⊙A的割线,
∴BN•BM=BP•BK.
∴
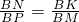
.
∵AK=BD,AK=MT,
∴BD=MT.
∵AD⊥BC,MT⊥BC,
∴∠ADB=∠MTC=90°.
∴∠C+∠CMT=90°.
∵∠BAC=90°,
∴∠C+∠ABC=90°.
∴∠ABC=∠CMT.
在△ABD和△CMT中,

,
∴△ABD≌△CMT.
∴AB=MC.
∵AK=AM,
∴AB+AK=MC+AM.
即BK=AC.
∴
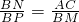
.
分析:(1)用角平分线的性质,圆的半径相等解题;
(2)根据图中相等角,找互余关系的角,从而推出垂直关系.
(3)连接PN,MK,根据已知证明△ABD≌△CMT再根据边之间的转化即可得到结论.
点评:本题考查了角平分线的性质,直角三角形两锐角互余,圆的割线定理,全等三角形的判定,综合性强.

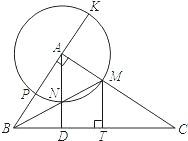 BM于N,AN的延长线交BC于D,直线AB交⊙A于P,K两点,作MT⊥BC于T.
BM于N,AN的延长线交BC于D,直线AB交⊙A于P,K两点,作MT⊥BC于T.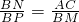 .
. 证明:(1)∵BM平分∠ABC,∠BAC=90°,MT⊥BC,
证明:(1)∵BM平分∠ABC,∠BAC=90°,MT⊥BC,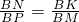 .
. ,
,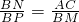 .
.

 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为