
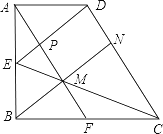
【题目】如图,已知直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC=2AD,点E、F分别是AB、BC边的中点,连接AF、CE交于点M,连接BM并延长交CD于点N,连接DE交AF于点P,则结论:①∠ABN=∠CBN;②DE∥BN;③△CDE是等腰三角形;④EM:BE= ![]() :3;⑤S△EPM=
:3;⑤S△EPM= ![]() S梯形ABCD , 正确的个数有( )
S梯形ABCD , 正确的个数有( )
A. 5个 B. 4个 C. 3个 D. 2个
【答案】B
【解析】连接DF,AC,EF,如图所示:
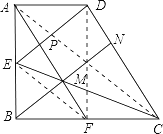
∵E、F分别为AB、BC的中点,且AB=BC,
∴AE=EB=BF=FC,
在△ABF和△CBE中,

∴△ABF≌△CBE(SAS),
∴∠BAF=∠BCE,AF=CE,
在△AME和△CMF中,
 ,
,
∴△AME≌△CMF(AAS),
∴EM=FM,
在△BEM和△BFM中,
 ,
,
∴△BEM≌△BFM(SSS),
∴∠ABN=∠CBN,选项①正确;
∵AE=AD,∠EAD=90°,
∴△AED为等腰直角三角形,
∴∠AED=45°,
∵∠ABC=90°,
∴∠ABN=∠CBN=45°,
∴∠AED=∠ABN=45°,
∴ED∥BN,选项②正确;
∵AB=BC=2AD,且BC=2FC,
∴AD=FC,又AD∥FC,
∴四边形AFCD为平行四边形,
∴AF=DC,又AF=CE,
∴DC=EC,
则△CED为等腰三角形,选项③正确;
∵EF为△ABC的中位线,
∴EF∥AC,且EF= ![]() AC,
AC,
∴∠MEF=∠MCA,∠EFM=∠MAC,
∴△EFM∽△CAM,
∴EM:MC=EF:AC=1:2,
设EM=x,则有MC=2x,EC=EM+MC=3x,
设EB=y,则有BC=2y,
在Rt△EBC中,根据勾股定理得:EC=![]() y,
y,
∴3x= ![]() y,即x:y=
y,即x:y= ![]() :3,
:3,
∴EM:BE= ![]() :3,选项④正确;
:3,选项④正确;
∵E为AB的中点,EP∥BM,
∴P为AM的中点,
∴S△AEP=S△EPM= ![]() S△AEM ,
S△AEM ,
又S△AEM=S△BEM , 且S△BEM=S△BFM ,
∴S△AEM=S△BEM=S△BFM= ![]() S△ABF ,
S△ABF ,
∵四边形ABFD为矩形,
∴S△ABF=S△ADF , 又S△ADF=S△DFC ,
∴S△ABF=S△ADF=S△DFC= ![]() S梯形ABCD ,
S梯形ABCD ,
∴S△EPM= ![]() S梯形ABCD , 选项⑤错误.
S梯形ABCD , 选项⑤错误.
则正确的个数有4个.
故答案为:B.


科目:初中数学 来源: 题型:
【题目】如图,分别位于反比例函数y=![]() ,y=
,y=![]() 在第一象限图象上的两点A,B,与原点O在同一直线上,且
在第一象限图象上的两点A,B,与原点O在同一直线上,且![]() .
.
(1)求反比例函数y=![]() 的表达式;
的表达式;
(2)过点A作x轴的平行线交y=![]() 的图象于点C,连接BC,求△ABC的面积.
的图象于点C,连接BC,求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=k1x+1与双曲线y=![]() 相交于P(1,m),Q(-2,-1)两点.
相交于P(1,m),Q(-2,-1)两点.
(1)求m的值;
(2)若A1(x1,y1),A2(x2,y2),A3(x3,y3)为双曲线上三点,且x1<x2<0<x3,请直接说明y1,y2,y3的大小关系;
(3)观察图象,请直接写出不等式k1x+1>![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c经过坐标原点,并与x轴交于点A(2,0)。
(1)求此抛物线的解析式;
(2)写出顶点坐标及对称轴;
(3)若抛物线上有一点B,且![]() ,求点B的坐标。
,求点B的坐标。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同时抛掷两枚硬币,按照正面出现的次数,可以分为“2个正面”、“1个正面”和“没有正面”这3种可能的结果,小红与小明两人共做了6组实验,每组实验都为同时抛掷两枚硬币10次,下表为实验记录的统计表:
结果 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 | 第六组 |
两个正面 | 3 | 3 | 5 | 1 | 4 | 2 |
一个正面 | 6 | 5 | 5 | 5 | 5 | 7 |
没有正面 | 1 | 2 | 0 | 4 | 1 | 1 |
由上表结果,计算得出现“2个正面”、“1个正面”和“没有正面”这3种结果的频率分别是___________________.当试验组数增加到很大时,请你对这三种结果的可能性的大小作出预测:______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点E(﹣4,2),F(﹣2,﹣2),以原点O为位似中心,位似比为2:1将△EFO缩小,则点E的对应点E′的坐标是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com