
【题目】如图,O是△ABC的内心,BO的延长线和△ABC的外接圆相交于D,连结DC、DA、OA、OC,四边形OADC为平行四边形.
(1)求证:△BOC≌△CDA.
(2)若AB=2,求阴影部分的面积.

【答案】(1)证明见解析;(2)![]() .
.
【解析】分析: (1)根据内心性质得∠1=∠2,∠3=∠4,则AD=CD,于是可判断四边形OADC为菱形,则BD垂直平分AC,∠4=∠5=∠6,易得OA=OC,∠2=∠3,所以OB=OC,可判断点O为△ABC的外心,则可判断△ABC为等边三角形,所以∠AOB=∠BOC=∠AOC=120°,BC=AC,再根据平行四边形的性质得∠ADC=∠AOC=120°,AD=OC,CD=OA=OB,则根据“SAS”证明△BOC≌△CDA;
(2)作OH⊥AB于H,如图,根据等腰三角形的性质和三角形内角和定理得到∠BOH=30°,根据垂径定理得到BH=AH=![]() AB=1,再利用含30度的直角三角形三边的关系得到OH=
AB=1,再利用含30度的直角三角形三边的关系得到OH=![]() BH=
BH=![]() ,OB=2OH=
,OB=2OH=![]() ,然后根据三角形面积公式和扇形面积公式,利用S阴影部分=S扇形AOB-S△AOB进行计算即可.
,然后根据三角形面积公式和扇形面积公式,利用S阴影部分=S扇形AOB-S△AOB进行计算即可.
详解:
(1)证明:∵O是△ABC的内心,

∴∠2=∠3,∠5=∠6,
∵∠1=∠2,∴∠1=∠3,
由AD∥CO,AD=CO,∴∠4=∠6,
∴△BOC≌△CDA(AAS)
(2)由(1)得,BC=AC,∠3=∠4=∠6,
∴∠ABC=∠ACB
∴AB=AC
∴△ABC是等边三角形
∴O是△ABC的内心也是外心
∴OA=OB=OC
设E为BD与AC的交点,BE垂直平分AC.
在Rt△OCE中,CE=![]() AC=
AC=![]() AB=1,∠OCE=30°,
AB=1,∠OCE=30°,
∴OA=OB=OC=![]()
∵∠AOC=120°,
∴![]()
=![]()
=![]()
点睛: 本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.也考查了等边三角形的判定与性质和扇形面积的计算.


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
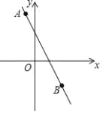
【题目】在直角坐标系中,一条直线经过A(﹣1,5),P(2,a),B(3,﹣3).
(1)求直线AB的函数表达式;
(2)求a的值;
(3)求△AOP的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
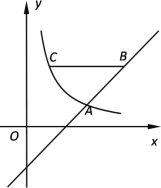
【题目】如图,在直角坐标系![]() 中,反比例函数图像与直线
中,反比例函数图像与直线![]() 相交于横坐标为3的点A.
相交于横坐标为3的点A.
(1)求反比例函数的解析式;
(2)如果点B在直线![]() 上,点C在反比例函数图像上,BC//
上,点C在反比例函数图像上,BC//![]() 轴,BC= 4,且BC在点A上方,求点B的坐标.
轴,BC= 4,且BC在点A上方,求点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
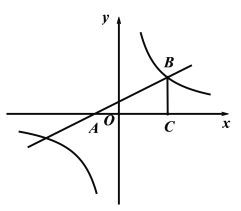
【题目】已知:如图,在平面直角坐标系xOy中,直线![]() 与x轴交于点A,在第一象限内与反比例函数图像交于点B,BC垂直于x轴,垂足为点C,且OC=2AO.求
与x轴交于点A,在第一象限内与反比例函数图像交于点B,BC垂直于x轴,垂足为点C,且OC=2AO.求
(1)点![]() 的坐标;
的坐标;
(2)反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在图1、图2中,线段AC=CE,点B是线段AC的中点,点D是线段CE的中点,四边形BCGF和CDHN都是正方形,AE的中点是M.如图1,点E在AC的延长线上,点N与点G重合时,点M与点C重合,容易证明FM=MH,FM⊥HM;现将图1的CE绕点C顺时针旋转一个锐角,得到图2,判断△FMH的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八(3)班全体同学参加植树苗活动,下面是今年3月份该班同学植树苗情况的扇形统计图和不完整的条形统计图:
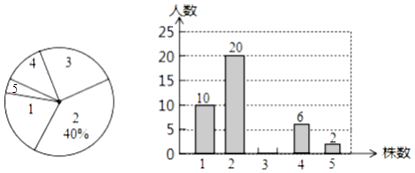
请根据以上统计图中的信息解答下列问题.
(1)该班同学共________人,植树苗3株的人数为________人;
(2)该班同学植树苗株数的中位数是________;
(3)小明用以下方法计算该班同学平均植树苗的株数是:![]() (株),根据你所学知识判断小明的计算是否正确,若不正确,请计算出正确的结果.
(株),根据你所学知识判断小明的计算是否正确,若不正确,请计算出正确的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,表中给出的是某月的月历,任意选取“H”型框中的7个数(如阴影部分所示),请你运用所学的数学知识来研究,发现这7个数的和不可能的是()
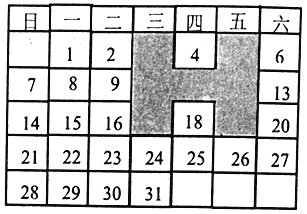
A.63B.70C.92D.105
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com