
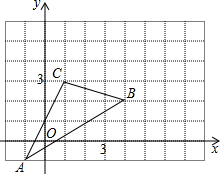
 如图,△ABC在直角坐标系中,
如图,△ABC在直角坐标系中,分析 (1)根据平面直角坐标系写出各点的坐标即可;
(2)根据网格结构找出点A、B、C平移后的对应点A′、B′、C′的位置,然后顺次连接即可,再根据平面直角坐标系写出各点的坐标;
(3)利用△ABC所在的矩形的面积减去四周三个小直角三角形的面积列式计算即可得解.
解答  解:(1)A(-1,-1),B(4,2),C(1,3);
解:(1)A(-1,-1),B(4,2),C(1,3);
(2)△A′B′C′如图所示,A′(1,1),B′(6,4),C′(3,5);
(3)S△ABC=5×4-$\frac{1}{2}$×5×3-$\frac{1}{2}$×1×3-$\frac{1}{2}$×2×4,
=20-7.5-1.5-4,
=20-13,
=7.
点评 本题考查了利用平移变换作图,熟练掌握网格结构准确找出对应点的位置是解题的关键.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
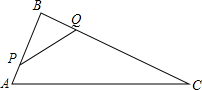 如图,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿AB向点B以2m/s的速度运动,点Q从点B开始沿BC边向点C以4cm/s的速度运动,如果P、Q分别从A、B同时出发,4秒后停止运动.则在开始运动后第几秒,△BPQ与△BAC相似?
如图,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿AB向点B以2m/s的速度运动,点Q从点B开始沿BC边向点C以4cm/s的速度运动,如果P、Q分别从A、B同时出发,4秒后停止运动.则在开始运动后第几秒,△BPQ与△BAC相似?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知△ABC是等边三角形,D、E分别是AB、AC边上的点,且DB=EC.
如图,已知△ABC是等边三角形,D、E分别是AB、AC边上的点,且DB=EC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com